Метод главных компонентов

Анализ главных компонент

Аппроксимировать данные линейными многообразиями меньшей размерности

Метод главных компонент (Principal componentan alysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ. KarlPearson) в 1901 г. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных. Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve) или преобразованием Хотеллинга (англ. Hotellingtransform). Другие способы уменьшения размерности данных — это метод независимых компонент, многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, метод упругих карт, поиск наилучшей проекции (англ.), нейросетевые методы «узкого горла», самоорганизующиеся карты Кохонена и др.

Проблемы PCA:

· Большой объем вычислений особенно на больших множествах данных

· Необходимость при получении новых данных полного пересчета не пространства покрывающих векторов, а полного пространства

· На выходе получается только линейное представление данных

Есть образцы данных. Осуществляем обучение. Хотим понизить размерность пространства, описывающего данные, за счет этого упростить анализ. Еще это надо делать автоматически. При это не надо потерять данные.

Все это делает PCA. Метод разработан Хоттелингом.

Метод главных компонент (Principal component analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Есть матрица Х, в которой строки – образцы. Есть целевой атрибут (нормальные/аномальные данные, класс атак). Хотим уменьшить количество атрибутов так, чтобы целевой атрибут определять.

Выбираем такие оси, вдоль которых наибольший разброс данных. Выбираем новые оси до тех пор, пока не получим разброс меньше заданного.

В результате осуществляется переход от большого количества параметров к небольшому количеству их линейных комбинаций. Задача человек – выбрать корректный набор атрибутов, в которых ищем. Например, нельзя использовать номера пакетов – разброс большой, а информации в нем нет.

Проблема - идет 1000 пакетов и в одном из них установлены все TCP флаги. Но по этому методу получится, что разброс будет не большим.

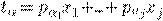
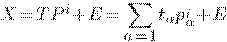
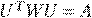
U – N*N собственные вектора матрицы.

W – матрица ковариаций образа.

При получении новых данных, требуется полный пересчет решения – итеративности не получится. На выходе получается только линейное представлении данных. Информации о корреляции удаляется при использовании PCA.

Дата добавления: 2014-01-15