ПФ как основа описания закономерностей производства

Общее представление об экономических моделях производства

ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ

Моделируемая экономическая система (ЭС) – совокупность «элементарных» экономических единиц, каждая из которых имеет определенную функцию, связанную с производством, потреблением, распределением или хранением материальных благ.

ЭММ производственно-технологического уровня ЭС описывает:

□ потоки ресурсов между элементарными экономическими единицами;

□ закономерности преобразования ресурсов и выпуска продуктов в этих единицах.

Потоки ресурсов между единицами выражаются в виде балансовых соотношений. Общий принцип построения балансовых соотношений: суммарное потребление любого продукта не превышает или равно сумме его исходных запасов производства в системе и поставок извне.

Если в модели две единицы, причем одна из них выпускает некоторый продукт в количестве у,который может быть сырьем в объеме x для второй единицы либо может вывозиться за пределы системы в количестве q, тогда:

q+х ≤ у,

где х – потребление второй единицей.

Если продукт у используется полностью (без остатка), то будет равенство:

q+x=y.

В описание потоков включают также ограничения на их величины (например, на пропускную способность транспортной сети).

Закономерности преобразования ресурсов и выпуска продуктов в производственных элементарных единицах описываются соотношениями, которые называются производственными функциями (ПФ).

ПФ – соотношение между производимой продукцией и используемыми ресурсами.

Модель ПФ включает:

1) n производственных ресурсов; х_i – количество i -го ресурса, i =1,…, n. Материальные производственные ресурсы различают по способам их расходования в процессе производства. Выделяют ресурсы двух типов: предметы труда (сырье) и основные фонды (здания, оборудование и т. д.). Ресурсы 1-го типа в процессе производства расходуются полностью в течение одного производственного цикла (периода выпуска продукции). Ресурсы 2-го типа (основные фонды) используются в течение нескольких циклов.

2) m производимых продуктов; y_j – объем выпуска j -гo продукта;

3) а = а ₁, а ₂,..., а_р – вектор параметров ПФ.

4) ПФ связывает вектор продукции y с вектором ресурсов х:

F(x, у, а) = 0. (1)

Соотношение (1) может быть векторным, т.е. из нескольких равенств.

Допущение: не учитывается продолжительность производственного цикла (т.е. периода между затратами ресурсов и выпуском продукции).

Описание элементарной производственной единицы (например, цеха) включает формулировку списка ресурсов и номенклатуры продукции с указанием значений и пределов изменения этих величин.

Два частных случая представления ПФ:

1. Функция выпуска. Независимые переменные – затраты ресурсов x:

y =f(х, а). (2)

В функции выпуска сочетаются различные количества ресурсов; один и тот же объем продукции может быть произведен при разных сочетаниях ресурсов.

2. Функция производственных затрат. Независимая переменная – выпуск y:

х =f^-1(y, а). (3)

В функции затрат задание выпуска продукции полностью определяет затраты ресурсов; отсутствует возможность замещения одного ресурса другим.

Функции выпуска и затрат – взаимно обратные.

Множество всех возможных сочетаний затрат ресурсов и выпусков продукции называется множеством производственных возможностей:

{ x, y }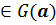. (4)

G(a) – некоторое множество G в пространстве ресурсов и продуктов, зависящее от вектора параметров a, 0 ≤ а ≤ 1.

Множество производственных возможностей задается соотношением:

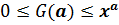(5)

Графическое представление :

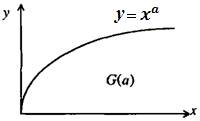
Существует связь между ПФ и множеством G(a):

для эффективного производства данному количеству ресурсов соответствует максимальное количество произведенной продукции, которое является границей множества производственных возможностей G(a), а именно функцией выпуска:

y = х^а, х > 0 (6)

Если производство данного объема продукции y достигается при минимальных затратах ресурса x, то получаем границу множества G(a) в виде функции затрат:

x = y ^{1/ а} , у > 0 (7)

Графическое представление функции затрат и множества G(a):

Соотношения (6) и (7) описывают одну и ту же зависимость, которая является границей множества производственных возможностей G(a) – множеством эффективных точек G(a).

В случае многокомпонентных величин x, у, a э ффективными точками множества G(a) являются такие объемы затрат x и выпуска у, которые удовлетворяют условиям:

1. При данных затратах x нельзя выпустить большее количество хотя бы одного вида продукции (у_j), не уменьшив производства других видов продукции.

2. Данного выпуска у нельзя добиться при меньших затратах хотя бы одного ресурса x_i, не увеличив при этом затраты других ресурсов.

3. Показатели предельного анализа ПФ

Рассмотрим ПФ выпуска y = f (х, а) с одним продуктом и несколькими ресурсами. Функция допускает замещение одного ресурса другим без изменения объема выпуска продукта y.

Будем считать, что параметры вектора а известны и их влияние не рассматриваем. Тогда функция выпуска приобретает вид:

y = f (х), (8)

где независимые переменные х =(х₁,...,х_п) – вектор затрат ресурсов.

Предположим, что ПФ задана при всех неотрицательных компонентах вектора х (х_i ≥ 0), является непрерывной (или нужное число раз дифференцируемой функцией своих аргументов).

Предельная производительность (эффективность) i-го ресурса (предельный продукт) – частная производная ПФ по одному из ресурсов 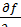. Характеризует скорость изменения функции выпуска по отношению к изменению затрат ресурса.

Если предельная производительность ресурса положительна (отрицательна), то при росте затрат ресурса выпуск растет (уменьшается).

Средняя производительность (эффективность) ресурса – показатель .

Эластичность выпуска по отношению к изменению затрат i-го ресурса:

является относительной характеристикой изменения выпуска продукции при увеличении затрат ресурса. Показывает, на сколько процентов возрастет выпуск продукции при увеличении затрат ресурсов на 1 %.

Величину ε _i (x) можно вычислить по другой эквивалентной формуле:

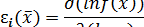
Определим показатели для ПФ вида y = х^а при х > 0.

Предельная эффективность ресурса:

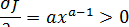
Средняя эффективность ресурса:

Так как 0 < а < 1, для этой ПФ предельная эффективность меньше средней.

Эластичность выпуска по ресурсу:

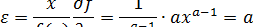
или .

Таким образом, ПФ y = х^а имеет постоянную эластичность выпуска по отношению к изменению затрат ресурса (ε = a).

Графики: ПФ y = х^а, предельной и средней эффективностей, эластичности выпуска по ресурсу.

Дата добавления: 2014-01-15