Основные допущения решения задач устойчивости

При определении критических нагрузок используются общепринятые допущения, приводящие реальные сооружения к идеализированным системам:

1) стержни системы до момента потери устойчивости испытывают только продольные деформации; внешняя нагрузка, действующая на стержневую систему, считается приложенной в узлах. Пренебрегая при этом укорочением сжатых и удлинением растянутых стержней, а также собственным весом ригелей в рамных системах, считают, что в таких системах до момента потери устойчивости не возникает изгиба (имеет место безмоментное напряженное состояние, т.е. ригели рам не напряжены, а стойки сжаты);

2) в момент потери устойчивости стержневой системы происходят угловые и линейные перемещения ее узлов, вызывающие деформации и усилия изгиба. При этом, как и в случае решения задач на прочность, не учитывают продольные деформации и деформации сдвига стержней рамных систем (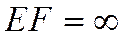, 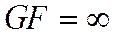), а также сближение их узлов при изгибе;

3) при потере устойчивости в «малом» (когда рассматриваются весьма малые перемещения) для решения задач можно использовать приближенное дифференциальное уравнение изогнутой оси стержня

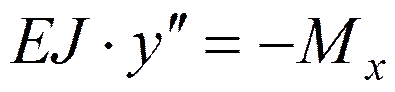(1.1)

вместо точного

,

не учитывая приращения продольных сил в момент потери устойчивости за счет изменения длины осевой линии;

4) стержневые системы считаются образованными из идеально прямых стержней, жестко или шарнирно соединенных между собой;

5) загружение системы предполагается простым, т.е. критическое состояние достигается одновременным возрастанием всех нагрузок и сохранением соотношения между ними.

Таким образом, при исследовании задач устойчивости реальное сооружение (механическая система) идеализируется, и в итоге изучается не сам механический объект, а дифференциальное уравнение, приближенно отражающее его действительные свойства.

Дата добавления: 2014-01-15