Лекция 2. Пример 1.Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР

Пример 1. Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР

РЕШЕНИЕ. Найдём ОР первого неравенства: . Построим прямую линию (рис. 1.2). Подставим координаты точки (0, 0) в неравенство: 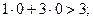так как координаты точки (0, 0) не удовлетворяют ему, то решением неравенства (1.1) является полуплоскость, не содержащая точку (0.0).

Аналогично найдём решения остальных неравенств системы. Получим, что ОР и ОДР системы неравенств является выпуклый многогранник АВСD.

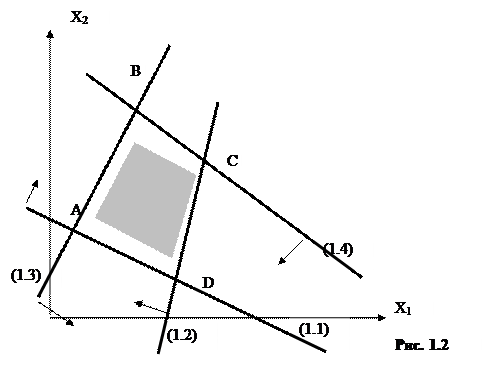Найдём угловые точки многогранника. Точку А определим как точку пересечения прямых

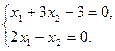
Решая систему, получим А(3/7, 6/7).

Точку В найдём как точку пересечения прямых

Из системы получим В(5/3, 10/3). Аналогично найдём координаты точек С и D: C(11/4, 9/4), D(21/10; 3/10).

Пример 2. Найти ОР и ОДР системы неравенств

РЕШЕНИЕ. Построим прямые и определим решения неравенств (1.5)-(1.7). ОР и ОДР являются неограниченные многогранные области ACFM и ABDEKM соответственно (рис. 1.3).

Пример 3. Найти ОР и ОДР системы неравенств

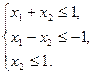
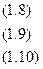
РЕШЕНИЕ. Найдём решения неравенств (1.8)-(1.10) (рис. 1.4). ОР представляет неограниченную многогранную область АВС; ОДР – точка В.

Пример 4. Найти ОР и ОДР системы неравенств

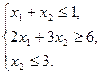
РЕШЕНИЕ. Построив прямые, найдём решения неравенств системы. ОР и ОДР не существует (рис. 1.5).

2. ГРАФИЧЕСКИЙ МЕТОД

Дата добавления: 2014-01-15