Синтез шифров

Классификация шифросистем:

1. По видам защищаемой информации (текст, речь, видео);

2. По способу построения (блочные, поточные);

3. По криптографическим характеристикам (стойкость);

4. По характеристикам программных и аппаратных реализаций.

Симметричное шифрование

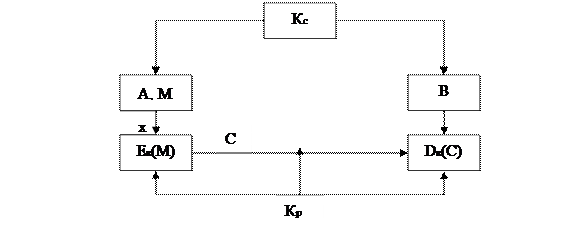
А – источник информации

В – получатель

М – сообщение, открытый текст

С – шифрованный текст

Ек(М) – некая функция шифрования

Dк(С) – функция расшифрования

Кр – криптоаналитик

Кс – секретный ключ

Зная С, Dк(С), Ек(М) на основе некоторой функции ψ(С) = (Х, Кс) получаем сообщение.

Для шифрования различных сообщений необходимо использовать различные ключи, поэтому у стороны А должна быть целая система ключей А{Кс,Ек}.

Требования к шифрам

1. Шифротекст читается только при наличии секретного ключа;

2. Число операций для определения секретного ключа по фрагменту шифротекста и такого же кусочка открытого текста должно быть не меньше общего числа возможных ключей, которое определяется как 2ⁿ, где n-разряд;

3. Знание алгоритма шифрования не должно влиять на надежность защиты;

4. Незначительное изменение ключа шифрования должно приводить к существенному изменению вида шифротекста;

5. Незначительное изменение открытого текста должно приводить к существенному изменению вида шифротекста, даже при использовании одного и того же секретного ключа;

6. Структурные элементы алгоритма шифрования должны быть неизменными (иначе не будет выполняться п. 4, 5);

7. Длина шифротекста должна быть равной длине исходного текста;

8. Не должно быть простых и легко устанавливаемых зависимостей между ключами, последовательно используемыми в процессе шифрования;

9. Любой ключ из множества возможных должно обеспечивать надежную ЗИ.

Все эти требования родились в систематизированном виде после публикации «Теории секретной передачи информации» Шеннона (1949-1950г.), где обосновывались теоретически криптостойкий алгоритм, практически криптостойкий алгоритм, а также принципы алгоритмов шифрования, обеспечивающие теоритическую и практическую криптостойкость. Таких принципов два. Они дают возможность выполнения данных 9 требований.

1. Принцип перемешивания. Шифрограмма не должна отличаться от случайного процесса;

2. Рассеивание (п. 5, 6, 7).

В основу практической реализации положены две операции: замена и подстановка. На выходе можно применить гаммирование.

Эти операции выполняются последовательно на каждом раунде, в результате чего происходит расширение ключа.

Асимметричное шифрование.

Алгоритм RSA (Revest, Shamir, Adelman) 1978г.

А – источник информации

В – получатель

М – сообщение

С – шифрованный текст

Еe(М) – функция шифрования сообщения М

Dd(С) – функция дешифрования

e, n – открытая информация

e – открытый ключ

e·d ≡ 1 mod m

e, d – взаимнообратные элементы

n = p·q, где p, q – простые числа

m = φ(n) – функция Эйлера

Формула шифрования: С = Мemod n

Формула дешифрования: М = Сdmod n

1<e, d<n

Особенности асимметричных систем:

1. Злоумышленнику, зная числа n,e, передаваемые по открытому каналу, вычислить М сложно. Однонаправленность функции С = Мemod n;

2. Числа в этом алгоритме должны быть достаточно большими (число десятичных знаков измеряется сотнями, в двоичном представлении – 1000 бит).

Алгоритм передачи секретного ключа по открытому каналу

В середине 70-х годов произошел настоящий прорыв в современной криптографии – появление асимметричных криптосистем, которые не требовали передачи секретного ключа между сторонами. Здесь отправной точкой принято считать работу, опубликованную Уитфилдом Диффи и Мартином Хеллманом в 1976г. под названием «Новые направления в современной криптографии». В ней впервые сформулированы принципы обмена шифрованной информацией без обмена секретным ключом.

У. Диффи и М. Хеллман предложили для создания криптографических систем с открытым ключом функцию дискретного возведения в степень.

КА, КВ – случайные числа

(а, р) Ек(а)

А	В
1. 1<к<p-2	1. 1<к<p-2
2. СА = акАmod р	2. СВ = акВmod р
3. А посылает В «СА»	3. В посылает А «СВ»
4. Вычисляется некоторое число, которое и является секретным ключом

к1 = СВкАmod р = акА·кВmod р;

к2 = САкВmod р = акА·кВmod р;

к1 = к2 = кс;

Не зная к1 и к2, злоумышленник может попытаться вычислить кс, зная только перехваченные СВ и СА. Эквивалентность этой проблемы в проблеме вычисления дискретного логарифма есть главный и открытый вопрос в системах с открытым ключом. Остается опасность имитации: злоумышленник может совершить подмену.

Алгоритм шифрования AES

1. История создания AES

2. Алгоритм шифрования

3. Математическое обоснование (использование полиномов над полем GF(2ⁿ), где n – 8 разрядов (байт)).

AES рассчитан на 32 разряда, обработка может идти побайтно. Вычисления проводятся по правилу конечного поля GF(2ⁿ). Используемые операции – сложение и умножение. Их можно связать между собой полиномом a_n-1· x^n-1…

Достоинство такого математического обоснования заключается в том, что все преобразования прозрачны, корректны. На основе математического обоснования можно оценить два принципа Шеннона: рассеивание и перемешивание.

В 1997 г. Американский Институт Стандартов объявил конкурс на создание нового стандарта криптографической защиты. В этом конкурсе принимали участие крупнейшие криптографы.

В 2001 г. был выбран определенный алгоритм: NIST (национальный институт стандартов).

Требования предъявляемые к алгоритму:

1. Алгоритм должен быть открыто опубликован. Он не должен быть запатентован.

2. Должен быть основан на использовании секретного ключа. k_c min 128, 192, 256 бит

3. Алгоритм должен быть предназначен для аппаратно программной реализации.

4. Область использования – любые программные продукты для защиты.

5. Криптоалгоритм должен быть изучен по следующим параметрам:

· Криптостойкость

· Стоимость

· Гибкость

· Реализуемость в смарт-картах

Криптостойкость – самый значимый параметр. Должен иметь статистическую безопасность. Криптограмма не должна отличаться от случайного процесса.

Алгоритм должен иметь широкую область использования, доступность, скорость действия (вычислительная эффективность), эффективность на различных платформах, удобство программно аппаратной реализации, прозрачность алгоритма шифрования;

Должна быть обеспечена возможность использования в алгоритме ключей различного формата, использования функций хэширования.

Смарт-карты используют небольшой объем памяти. Должна быть возможность расширения ключа на лету.

На конкурс были приняты 15 алгоритмов из 12 стран мира. После 1 тура были отобраны 6 алгоритмов:

1. MARS – IBM (США)

2. TWOFISH (США)

3. RC6 (США)

4. RIJNDAEL (Бельгия) – победитель

5. SERPENT (Великобритания)

MARS

«+»: высокий уровень защищенности, высокая эффективность на 32-разрядных платформах, ключ рассчитан на 256 бит.

«-»: сложно оценить криптостойкость, сложен анализ надежности.

RC6

«+»: высокая эффективность на 32-битовых платформах, простая структура алгоритма упрощает анализ надежности, наличие предшественника RC5, быстрая процедура формирования ключа.

«-»: нет возможности расширения ключа на лету.

TWOFISH

«+»: таблица замены.

«-»: большая сложность, затруднен криптоанализ.

SERPENT – самый медленный среди финалистов.

RIJNDAEL

Именно на этом алгоритме сошлись все участники конкурса в качестве стандарта. У этого алгоритма существовал прототип.

«+»: высокая эффективность на любых платформах, высокий уровень защищенности, хорошо подходит для реализации в смарт-картах из-за низких требований к памяти, быстрая процедура расширения ключа, хорошая поддержка параллелизма, поддержка разных бит ключа шагом 32 бит до 256.

«-»: уязвим к анализу мощности.

Алгоритм вступил в силу в мае 2002 г. формальное название FIPS (Federal Information Proccessing Standart).

Суть алгоритма.

Архитектура – квадрат. Исходный массив (128 бит) предстает в виде матрицы. Обработка возможна как побайтно, так и по 32 разряда. Ключ предстает также в виде матрицы (матрица ключа). взаимодействие с ключом производится по столбцам.

М₁ М₂ М₃ М₁ М₂ – 32 разряда

8б

Перед взаимодействием с ключом производятся три операции, реализуемые по правилу поля GF(2³²) – поразрядно.

Операции:

1. Операция замены – нелинейное преобразование байта. Исходные 8 бит заменяются новыми 8 битами.

X = A_8*8 X′ + B

X – 8-разрядный вектор, который является нелинейным преобразованием.

Х′ - исходное состояние

В - константа

2. Операция сдвига строк. Первая строка не меняется, вторая строка сдвигается на 1 байт, следующая на 2 байта. В результате получится новая матрица

3. Перемешивание столбцов – перестановка столбцов.

После выполнения этих трех операций производится сложение с ключом. Выполнение данных четырех операций составляет 1 раунд. Всего в алгоритме осуществляется 10 раундов.

Дата добавления: 2014-01-15