
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм Blowfish
|
|
|
|
Алгоритм Blowfish разработал американец Б. Шнайер. Данный алгоритм базируется на сети Фейстелл, не запатентован. Многораундовый (18 раундов) алгоритм обрабатывает 32-разрядные числа.
Основная функция – операция сложения.
kc<448 бит>
Ключ разворачивается предварительно, не на лету. Достаточно криптостойкий.
Предварительно формируется массив ключей 448*18.
18 32-разрядных слов (подключей) p1,p2,…,p18. Каждый pi – четыре 32-разрядных вектора. Используется табличное преобразование (нелинейное), применение 32х s-блоков. Каждый s-блок – 256 элементов.
s10, s11,...,s1,255
s20, s21,...,s2,255
s30, s31,…,s3,255
s40, s41,…,s4,255
Блок-схема
<64 To>





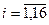



Перестановка 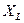 и
и 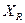
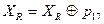
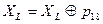
Функция F


Алгоритм расширения ключа
1. Исходный ключ получается с помощью ПЧС.
2. Выполняется XOR p1 c первыми 32-разрядными битами ключа; XOR p2 – со вторыми 32-разрядными битами и т.д. до p18.
3. Шифрование алгоритмом Blowfish
4. p1 и p2 заменяются результатом шага 3.
5. Результат этапа 3 шифруется с помощью алгоритма Blowfish и измененных подключей.
6. p3 и p4 заменяются результатом этапа 5.
7. Все элементы p-массива заменяются выходом, постоянно меняющимся.
В алгоритмах DES и ГОСТ таблицы фиксированы, а в Blowfish заключается в том, что ключи формируются в зависимости от исходных данных.
ГОСТ 28147 – 89
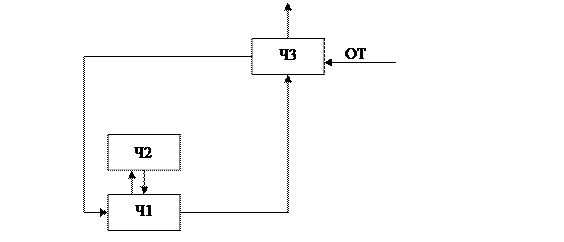
Структура алгоритма состоит из трех частей. Предназначен для реализации блочного шифрования. Каждый блок – 64 бита. 64 бита открытого текста преобразуется в 64 биташифрованного текста. М разбивается в двоичном представлении.
 М→ М1, М2 …, Мк
М→ М1, М2 …, Мк
С1, С2 …, Ск
Мi
OT <64>
Ci
ШТ <64>
Степень стойкости зависит от режима.
Все три части используют три основные операции:
· Поразрядное сложение по mod 2 
· Сложение двух чисел a, b (32 разряда каждое) (a+b) mod 232 
· Сложение (a+b) mod (232-1) 
Часть1 – базовый блок.
Режим работает следующим образом. В часть заносится 64 бита, которые делятся попалам. Далее над ними выполняются операции. Всего проводится 32 раунда. После 32 раундов получаем из М1→ С1. такой режим называется заменой.
Структура Ч1 при реализации алгоритма замены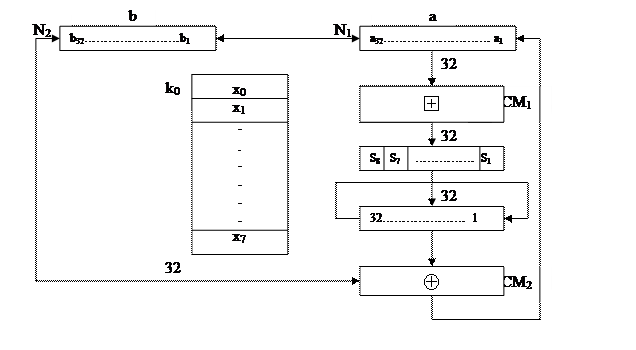
В регистры N1 и N2 заносятся числа a, b. Регистры связаны между собой. Исходные 64 бита представляются в виде a1…a32, b1…b32. Память с ключом – 256 бит. Память состоит из 8 ячеек по 32 разряда. CM1 – сумматор, реализующий операцию  . Далее следует блок памяти, реализующий нелинейную операцию. Регистр сдвига осуществляет сдвиг на 11 разрядов (своего рода перемешивание). CM1 – сумматор, реализующий сложение по mod 2. Из N1 значения выталкиваются в N2. Таким образом осуществляется один раунд. Также происходят следующие раунды, но во втором раунде в качестве ключа берется х1, в третьем – х2 и т.д. Так происходит каждые 8 раундов. Но на последнем раунде использование ключей меняется ключи берутся в обратном порядке.
. Далее следует блок памяти, реализующий нелинейную операцию. Регистр сдвига осуществляет сдвиг на 11 разрядов (своего рода перемешивание). CM1 – сумматор, реализующий сложение по mod 2. Из N1 значения выталкиваются в N2. Таким образом осуществляется один раунд. Также происходят следующие раунды, но во втором раунде в качестве ключа берется х1, в третьем – х2 и т.д. Так происходит каждые 8 раундов. Но на последнем раунде использование ключей меняется ключи берутся в обратном порядке.
| Цикл | Исходное состояние а(0), b(0) |
| j = 1 – 24 j = 25 – 31 |
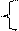 a(1) = φ(a(0) a(1) = φ(a(0)  k0) k0)  b(0)
b(1) = a(0) b(0)
b(1) = a(0)
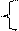 a(j) = φ(a(j-1) a(j) = φ(a(j-1)  kj-1(mod 8)) kj-1(mod 8))  b(j-1)
b(j) = a(j-1) b(j-1)
b(j) = a(j-1)
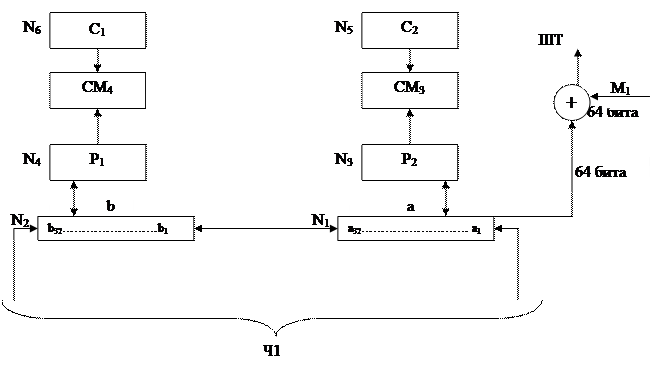
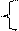 a(j) = φ(a(j-1) a(j) = φ(a(j-1)  k32-1) k32-1)  b(j-1)
b(j) = a(j-1) b(j-1)
b(j) = a(j-1)
|
После 32 раунда a(32) = a(31), b(32) = φ(a(31) + k0)  b(31)
b(31)
Базовая часть служит для режима гаммирования.
Часть 1 предназначена для формирования данных.
N5, N6 – 32-разрядные регистры
С1, С2 – константы
Для получения гаммы используется СМ4(С1,N4)
Хэш-функция базируется на этом алгоритме
Отечественный стандарт предполагает 4 режима:
1. Режим замены (r1);
2. Режим гаммирования (r1, r2,r3);
3. Режим гаммирования с обратной связью (r1,r3);
4. Имитовставка
Режим гаммирования с обратной связью.
Схема реализующая гаммирование с обратной связью, имеет следующий вид:
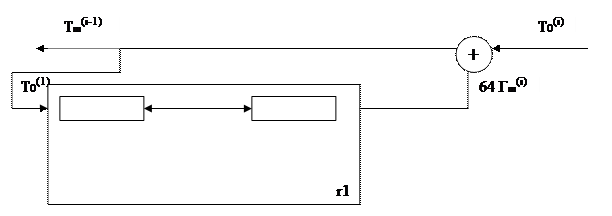
Открытые данные, разбитые на 64-разрядные блоки Т0(1),Т0(2), зашифровываются путем поразрядного сложения по модулю 2 с гаммой шифра Гш, которая вырабатывается блоками по 64 бита.
Число двоичных разрядов в блоке Т0(i) может быть менее 64, при этом неиспользованная дел шифрования часть гаммы шифра из блока Гш(i) отбрасывается.
Имитовставка.
Имитовсатавка – это блок из Р бит, который вырабатывают по определенному правилу из открытых данных с использованием ключа и затем добавляют к зашифрованным данным для обеспечения их имитозащиты.
Имитозащита – это защита системы шифрованной связи от навязывания ложных данных.
Имитовставка вырабатывается из блоков открытых данных либо перед шифрованием всего сообщения, либо параллельно с шифрованием по блокам.
< М1,…, Мm>
< С1, …, Сm>
Берется несколько блоков С′к …С′m – зашифрованных. Блоки подвергают преобразованию, соответствующему первым 16 циклам алгоритма зашифрования в режиме простой замены.
p = < С′к …С′m > - имитовставка
Получателю пересылается < С1, …, Сm, р>. Поступившие к получателю зашифрованные данные расшифровываются, и из полученных блоков открытых данных вырабатывается имтовставка. Эта имитовставка сравнивается с имитовставкой, полученной вместе с зашифрованными данными. В случае несовпадения имитовставок полученные при расшифровании блоки открытых данныхт считают ложными.
С помощью имитовставок проверяются:
1. целостность исходного текста;
2. аутентификация;
3. юридическая подпись.
Американский стандарт шифрования DES.
Стандарт шифрования данных DES(Data Encryption Standart) опубликован в 1977г. Национальным бюро стандартов США.
Основные достоинства алгоритма DES:
1. используется только один ключ длиной 56 бит;
2. зашифровав сообщение с помощью одного пакета программ, для расшифровки можно использовать любой другой пакет программ, соответствующий стандарту DES;
3. относительная простота алгоритма обеспечивает высокую скорость обработки;
4. достаточно высокая стойкость алгоритма.
Алгоритм DES использует комбинацию подстановок и перестановок. DES осуществляет шифрование 64-битовых блоков данных с помощью 64-битового ключа, в котором значащими являются 56 бит (остальные 8 бит – проверочные биты для контроля на честность).
Обобщенная схема процесса шифрования в алгоритме DES.
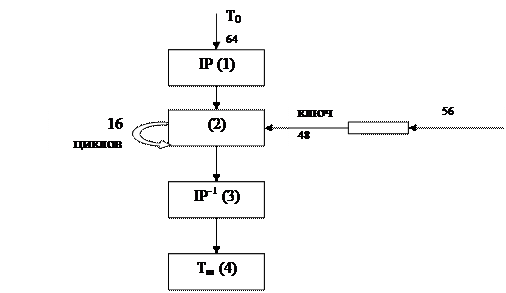
1. начальная перестановка
2. шифрование
3. конечная перестановка
4. шифротекст
64-битовый блок Т образуется с помощью матрицы начальной перестановки IP.
Биты входного блока Т(64 бита) переставляются в соответствии с матрицей IP: бит 58 входного блока Т становится битом 1, битом 2 и т.д. Полученная последовательность битов Т0 разделяется на две последовательности: L0 – левые или старшие биты, R0 – правые или младшие биты, каждая из которых содержит 32 бита.
По окончании шифрования осуществляется восстановление позиций битов с помощью матрицы обратной перестановки IP-1.
Реализация шифрования.
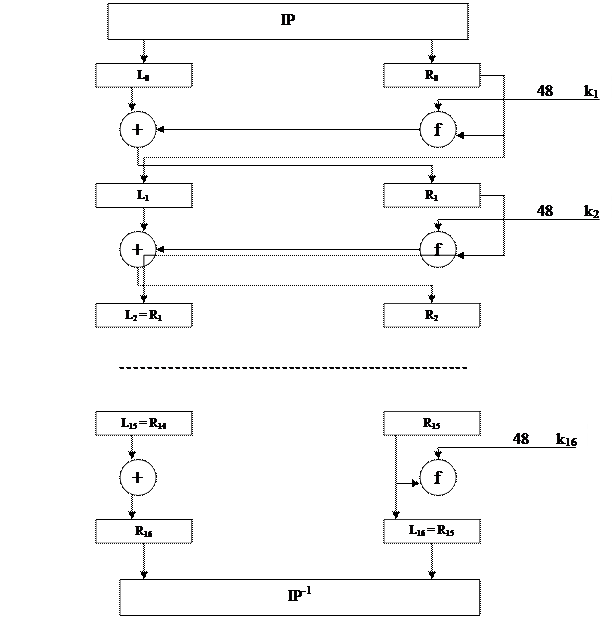
R1 = L0  f(R0,k1)
f(R0,k1)
…………………..
R16= L15 f(R15,k16)
f(R15,k16)
f – функция шифрования
Достигаются принципы Шеннона: перемешивания и рассеивания.
Рассеивание – изменение хотя бы одного бита в открытом тексте в раунде влечет изменение на выходе до пяти бит. После 16 раундов рассеивание полное, влияние на все 64 бита.
В 70-е гг. 1 раунд – сеть Фейстеля.
Принципы Шеннона достигаются благодаря тому, что:
1. преобразования представляются в виде сети Фейстеля;
2. чередование процедур;
3. итеративный процесс реализуется 16 раундов.
Главное требование – обратимость преобразования. Обратимость основана на использовании операций подстановки, перестановки, замены они по определению обратимы.
Алгоритм Эль- Гамаля.
1985 г. Алгоритм Эль- Гамаля основан на проблеме дискретного логарифма. Для вскрытия перебором необходимо 1026 логических операций.

 Q, P
Q, P
| А | В к0 кCB |
| M, Q, P, e | Q, P, e d |
1.  подготавливает секретное число для шифрования 1<кСА<p-1
(кСА,p-1) = 1 подготавливает секретное число для шифрования 1<кСА<p-1
(кСА,p-1) = 1
| e = y = QкCB mod р d = кCB 1<кСB<p-1 |
2.  С1 = QкСА mod р С1 = QкСА mod р
| |
| 3. С2 = (yкСА · M) mod р |
4.  (C1, C2)
(C1, C2)
Открытыми являются два вспомогательных числа Q и P
1<Q<p-1
C1, C2 → M = (C2/C1кCB) mod p
(yкСА · M/QкСА· кСB) mod p = (QкСА· кСB · M/QкСА· кСB) mod p = M mod p
Пример:
P = 11, Q = 2, M= 5
| А: кСА = 9 | В: кCB = 8 |
 С1 = 29 mod 11 = 6 С1 = 29 mod 11 = 6
| e = y = 28 mod 11 = 3 |
| С2 = (39 · 5) mod 11 = 9 | |
 (6,9) (6,9)
| (9·(68)-1) mod p = 5 |
Электронно-цифровая подпись (ЭЦП)
Выполняет такую же роль, как и собственноручная подпись.
Функции:
1. Авторство;
2. Целостность;
3. Аутентификация.
| ||
|
Ф1 – некий документ
Ф2 – приложение к Ф1
Цифровая подпись (ЦП) – дополнительный файл, отражающий данные не только об источнике, но и данные о документе.
Ф2 = у = (М, кс), где с – некие секретные данные
Алгоритм постановки подписи выполняет сторона А. Реализует алгоритм проверки подписи сторона В.
ЦП на основе алгоритма RSA
Используется функция хэширования Н(М) = m << M
| B: |
| e, n, M, C |
| m′ = Ce mod n |
| m = H(M) |
| Проверяет m = m′ |
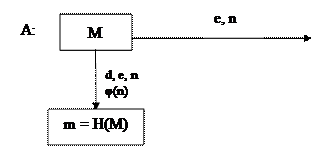
(этап хэширования)
 |
C = md mod n =

 (C, M)
(C, M)
Аналогичным образом происходит действие и по алгоритму Эль-Гамаля. Здесь также необходимо использовать функцию хэширования Н(М).
ЦП на основе алгоритма Эль-Гамаля
 А: Q, P, M А: Q, P, M
| В: Q, P, y |
| 1. 1<kСА<p-1 | (M, С1, С2) |
2.  e = y = QkCB mod р
3. m = H(M)
4. 1<k<p-1, (k, p-1) = 1
5. С1 = Qк mod р
6. m = (kСА·C1 + k·C2) mod (p-1)
Находим С2 e = y = QkCB mod р
3. m = H(M)
4. 1<k<p-1, (k, p-1) = 1
5. С1 = Qк mod р
6. m = (kСА·C1 + k·C2) mod (p-1)
Находим С2
 (С1, С2) (С1, С2)
| 1. m = H(M) 2. A = (yС1·C1С2) mod p 3. A = Qm mod p 4. A = A′ |
Дополнение к RSA.
1. Почему работает RSA
Х – ОТ
Y – ШТ
A: y = (ax + b) mod m,
m – число букв в алфавите
а,b – некоторые числа
k = (a,b) – ключ
B: x = Ek(y) = [(y + (m-b))·a-1] mod m
a→ a-1
Если m – простое число, то a-1 есть у каждого элемента из 1…(m-1).
Если (a,m) = 1, то не будет совпадений в значениях зашифрованного текста.
Чтобы однозначно поставить в соответствие С и М, требуется k1 k2
e · d ≡ 1 mod φ(m)
Ek1(M) = C
Dk2(C) = M
С = Me mod m; m = p·q
a ≡ b mod m; a·b = m·k + r
M<m; (M,m) = 1;
Сd mod m = M = Me·d mod m = M(1+φ(m)k) mod m = M · Mφ(m)k mod m = M mod m,
так как e·d ≡ 1 mod φ(m)
e·d = 1 + φ(m)·k,
aφ(m)k ≡ 1k mod m, (a,m) = 1
Необходимо доказать, что p·q | Med - M для любых М
Med mod p = M mod p
Med mod q = M mod q
p| Med - M
q| Med - M
(M · Mφ(m)k) mod p = M · M(p-1)(q-1)k mod p = M mod p
(M · Mφ(m)k) mod q = M · M(p-1)(q-1)k mod q = M mod q
M · M(p-1)(q-1)k mod p = 1
M · M(p-1)(q-1)k mod q = 1
Следовательно, p·q| Med – M. По теории сравнимости: если одно Ито же число делится на p и на q, то оно делится и на их произведение.
2. Выбор p и q
p = 2p - 1 – нельзя брать такое р
Получение простых чисел для алгоритма RSA
r, s, t – простые числа
Число р называется простым устойчивым, если оно удовлетворяет следующим условиям:
1. р ≡ 1 mod r
2. p ≡ (s-1) mod s
3. r ≡ 1 mod t
Числа r, s, t должны удовлетворять следующим критериям:
1. r ≡ (u-1) mod u
2. s ≡ 1 mod w
3. s ≡ (v-1) mod v, где u, v, w – простые числа
Пример:
р = 19819 = 2·3·3·17·653 + 1 = 2·2·5·97·103-1
р – устойчивое простое число
Процедура получения устойчивых простых чисел
1. Генерируются простые числа s,t
2. Получаем простое число r такое что, (r-1) делит t без остатка: r-1|t
На основе этих двух операций получаем простое число р по следующей формуле:
P = U(r,s) + krs, где k – подборное натуральноге число
Число р должно удовлетворять следующим свойствам:
· p ≡ 1 mod r
· p ≡ (s-1) mod s
· U(r,s) = (sr-1 – rs-1) mod rs
Цифровая подпись DSA (Digital Standart Alhoritm)
Появилась в 1991 г. Основана на базе подписи Эль – Гамаля.
Исходные числа – три простые числа G, P(512-1024 бит), Q(160 бит).
q|p-1
| А: | В: |
| 1. Формирует случайное число х 1<x<q | 1. Вычисляет w = 1s mod q |
2. Вычисляет y (открытый ключ) y = Gx mod р
3. Хэширование m = h(M)
1<m<q
4. Формирует случайное число kA 1< kA <q
5. Вычисляет число r
r = (GkA mod р) mod q
6. Вычисляет число s
s = (m+rx/ kA) mod q
ЭЦП – (r,s)
7. (r, s, m)
| 2.  m = h(M)
3. U1 = (m·w) mod q
U2 = (r·w) mod q
4. v = ((GU1·yU2) mod p) mod q
5. Проверка равенства
v = r m = h(M)
3. U1 = (m·w) mod q
U2 = (r·w) mod q
4. v = ((GU1·yU2) mod p) mod q
5. Проверка равенства
v = r
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2504; Нарушение авторских прав?; Мы поможем в написании вашей работы!