Лекция №12

Полиномиальные преобразования в поле это число подписанное GF(2)

Хэш-функция (безключевая)

Сжимать информацию можно без ключа

h(M) = m – фиксированное число бит

Пример – конечный полуавтомат (задача одна функция перехода).

Если большое число состояний, например, 2²⁵⁶, то реализация очень сложна.

Хэш-функция может быть реализована на основе полинома. Назначение – проверка целостности.

Вероятность ошибки p(∆) = 1/2²⁵⁶

Реализация проверки целостности на основе полинома. Сообщение M_i - последовательность бит.

M_i ψ (x) = a₀x^n-1 + a₁x^n-2 + … + a_n-2x + a_n-1

ψ (x) = φ(x) · g(x) + R(x) (1)

φ(x) – делитель

g(x) – частное

R(x) – остаток

R(x) представляется в виде полинома.

Остаток R(x) есть значение хэш-функции.

(1)хорошо реализуется на основе двоичных полиномов. В основе реализации – сдвиговый регистр.

Пример реализации получения остатка.

CRC-коды – для проверки целостности

L – используемого регистра

Двоичный полином предстает в виде набора коэффициентов

f(x) a (вектор коэффициентов)

а = (10101100010) – 11 бит

φ(x) обычно предстает в виде примитивного полинома, имеющего максимальный период L = 2ⁿ – 1

φ(x) = x⁴ + x + 1 10011

ψ(x) = x¹⁰ + x⁸ + x⁶ + x⁵ + x

x¹⁰ + x⁸ + x⁶ + x⁵ + x x⁴ + x + 1

x¹⁰ + x⁷ + x⁶ x⁶ + x⁴ + x³

x⁸ + x⁷ + x⁵ + x

x⁸ + x⁷ + x⁴

x⁷ + x⁴ + x

x⁷ + x⁴ + x³

x³ + x - R(x)

В двоичном представлении

10101100010 10011

10011 1011

11010

10010

1010 - R(x)

Реализация с помощью сдвигового регистра.

10011 – характеристический полином, который определяет обратную связь, где реализуется сложение по модулю 2.

Для деления и умножения используется регистр сдвига следующим образом:

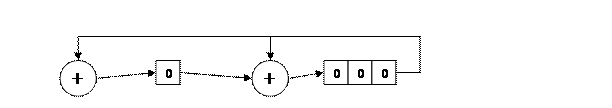
а 1 1 000

0 0 100

1 1 010

0 0 101

1 0 110

1 1 011

0 1 011

0 1 001 - частное g(x)

0 1 000

0 0 100

1 1 010

0 0 101 R(x)

Примитивных полиномов может быть несколько. В данном случае их два. При использовании другого примитивного полинома остаток R(x), естественно, будет другой.

Передача К_С для симметричных криптосистем по открытому каналу.

1. Алгоритм Диффи-Хеллмана

А® В: а^Кса mod p=c₁

B® A: a^Kcв mod p=c₂

K=a^{Kca * Kcв} mod p

Этот алгоритм двухраундовый. Недостатком является то, что криптоаналитик может перехватить а ^Kca, a^Kcв и заменить, может выступить как сторона А, так и как сторона В.

Однораундовый алгоритм.

А:K_са® В:Е В:К₀®А К₀=Q^Kcв mod p

E_K0(K_ca, t, A)®В С=Е_К0 (К_са, t, A)

¯

K_ca=D_K0(C)

Сторона А инициирует передачу.

Недостаток: нет части, на основе которой можно проверить подлинность.

Протокол передачи К_с с аутентификацией.

Шаг 1. A®B: E_Koв(k₁, A); B®A: K_oв;

Шаг 2. B®A: E_Koa(k₁, k₂); A®B: K_oa;

Шаг 3. A®B: E_Koв(k₂);

k_c=k₁;

Шаги 2,3 предназначены для аутентификации.

Модификации алгоритма Диффи-Хеллмана.

Дата добавления: 2014-01-15