Сеть Фейстеля

(Horst Feistel 1915-1990 гг)

Большинство современных блочных шифров используют сеть Фейстеля в качестве основы. Альтернативой сети Фейстеля является подстановочно-перестановочная сеть.

Исторически, первым алгоритмом, использующим сеть Фейстеля, был алгоритм Люцифер, при работе над которым Фейстелем и была, собственно, разработана структура, которую затем стали называть «сетью Фейстеля». В июне 1971 года Фейстелем был получен американский патент № 3798359.

Дальнейшей модификацией метода смешивания текущей части шифруемого блока с результатом некоторой функции, вычисленной от другой независимой части того же блока является сеть Фейстеля. Она получила широкое распространение, поскольку обеспечивает выполнение требования о многократном использовании ключа и материала исходного блока информации.

Классическая сеть Фейстеля имеет структуру, где независимые потоки информации, порожденные из исходного блока, называются ветвями сети. В классической схеме их две. Величины V_i именуются параметрами сети, обычно это функции материала ключа. Функция F называется образующей. Действие, состоящее из однократного вычисления образующей функции и последующего наложения ее результата на другую ветвь с обменом их местами, называется циклом или раундом сети Фейстеля. Оптимальное число раундов R – от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптостойкость любого блочного шифра к криптоанализу. Возможно, эта особенность и повлияла на столь активное распространение сети Фейстеля – ведь при обнаружении, скажем, какого-либо слабого места в алгоритме, почти всегда достаточно увеличить количество раундов на 4–8, не переписывая сам алгоритм. Часто количество раундов не фиксируется разработчиками алгоритма, а лишь указываются разумные пределы (обязательно нижний и не всегда верхний) этого параметра.

Данная схема является обратимой, поскольку сеть Фейстеля обладает тем свойством, что даже если в качестве образующей функции F будет использовано необратимое преобразование, то и в этом случае вся цепочка будет восстановима. Это происходит вследствие того, что для обратного преобразования сета Фейстеля не нужно вычислять
функцию F^-1.

Более того, сеть Фейстеля симметрична. Использование операции XOR, обратимой своим же повтором, и инверсия последнего обмена ветвей делают возможным раскодирование блока той же сетью Фейштеля, но с инверсным порядком параметров V_i. Заметим, что для обратимости сети Фейстеля не имеет значение, является ли число раундов четным или нечетным числом. В большинстве реализаций схемы, в которых операция XOR и уничтожение последнего обмена сохранены, прямое и обратное преобразования проводятся одной и той же процедурой, которой в качестве параметра передается вектор величин V_i либо в исходном, либо в инверсном порядке.

Пусть X – блок информации (длина блока в битах обязательно должна быть четной). Представим его в виде двух подблоков одинаковой длины X ={A, B}. Один раунд сети Фейстеля определяется как математическое преобразование

,

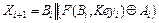где || – операция конкатенации (сцепления), – побитовое исключающее ИЛИ (XOR)

Структура одной итерации сети Фейстеля показана на рис. 5.

Хорст Фейстель описывает два различных блока преобразований (функций 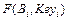) — блок подстановок (S -блок) и блок перестановок (P -блок). Можно показать, что любое двоичное преобразование над двоичным блоком фиксированной длины, сводятся к S -блоку, но на практике в силу сложности строения n-разрядного S -блока при больших n, применяют более простые конструкции.

В блоке подстановок (S-блок) используется генерируемая таблица замены

Таблица замены для приведённого 3-разрядного S-блока № комбинации

0 1 2 3 4 5 6 7

Вход 000 001 010 011 100 101 110 111

Выход 011 000 001 100 110 111 010 101

Блок перестановок P -блок (P -box) всего лишь изменяет положение цифр и является линейным устройством.

Циклический сдвиг является частным случаем P-блока. В простейшем случае (сдвиг на 1 бит), крайний бит отщепляется и перемещается на другой конец регистра или шины. В зависимости от того, какой бит берётся, правый или левый, сдвиг называется вправо или влево. Сдвиги на большее число бит можно рассматривать, как многократное применение сдвига на 1.

Сеть Фейстеля состоит из фиксированного числа итераций, определяемого соображениями стойкости разрабатываемого шифра, при этом на последней итерации перестановка местами половин блоков текста не производится, так как это не влияет на стойкость шифра.

Данная структура шифров обладает рядом достоинств, а именно:

- процедуры шифрования и дешифрования совпадают, с тем исключением, что при дешифровании ключевая информация используется в обратном порядке;

- для построения устройств шифрования можно использовать те же блоки в цепях шифрования и дешифрования.

Недостатком является то, что на каждой итерации изменяется только

половина обрабатываемого текста, что приводит к необходимости увеличивать число итераций для достижения требуемой стойкости.

В отношении выбора F -функции определенных стандартов не существует, однако, как правило, эта функция представляет собой последовательность зависящих от ключа нелинейных замен, перемешивающих перестановок и сдвигов.

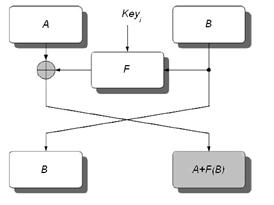
Рис. 5. Структура одной итерации сети Фейштеля

С незначительными доработками сеть Фейстеля можно сделать и абсолютно симметричной, то есть выполняющей функции шифрования и дешифрования одним и тем же набором операций.

Как известно, основные единицы информации, обрабатываемые процессорами на сегодняшний день – это байт и двойное машинное слово 32 бита. Поэтому в блочных криптоалгоритмах встречается сеть Фейстеля с 4-мя ветвями. Для более быстрого перемешивания информации между ветвями (а это основная проблема сети Фейстеля с большим количеством ветвей) применяются две модифицированные схемы.

Сеть Фейстеля надежно зарекомендовала себя как криптостойкая схема произведения преобразований, и ее вы имеете возможность найти практически в любом современном блочном шифре. Незначительные модификации касаются обычно дополнительных начальных и оконечных преобразований над шифруемым блоком. Подобные преобразования, выполняемые обычно также либо «исключающим ИЛИ» либо сложением, имеют целью повысить начальную рандомизацию входного текста. Таким образом, криптостойкость блочного шифра, использующего сеть Фейштеля, определяется на 95% функцией F и правилом вычисления V_i из ключа. Эти функции и являются объектом все новых и новых исследований специалистов в области криптографии.

Примеры некоторых блочных шифров и их основные параметры приведены в таблице 5.

До принятия в качестве стандарта алгоритма AES во многих странах, в том числе и в США до начала XXI века, использовался алгоритм DES. Несмотря на множество найденных криптоаналитических методов, применимых к DES, за 25 лет фактически не было обнаружено каких-либо серьезных уязвимостей в данном алгоритме, за исключением одного, но весьма принципиального недостатка: весьма короткого ключа, реальный размер которого составляет всего 56 бит. Насколько это мало, можно судить из следующей весьма распространенной оценки: для полного перебора ключей DES достаточно примерно 20 часов работы миллиона процессоров, каждый из которых перебирает миллион ключей DES в секунду [13]. Ясно, что такой стойкости против вскрытия алгоритма методом «грубой силы» в современных условиях недостаточно.

Одним из последних шифров является AES. В отличие от многих других криптографических стандартов, например, стандарта шифрования США DES или отечественного стандарта ГОСТ 28147-89, AES не был разработан «в недрах спецслужб», а выбран на открытом конкурсе из относительно большого числа алгоритмов-претендентов в 2000 г.

Таблица 5. Наиболее популярные блочные шифры

Название шифра	Исторические сведения	Основные характеристики
DES – Data Encryption Standard (стандарт шифрования данных)	Разработан в середине 70-х годов сотрудником корпорации IBM Х. Фейстелем	Данный шифр основан на сети Фейштеля. Шифруется блок из 64 бит, используется 64-битовый ключ (требуется только 56 бит), 16 проходов. Может работать в 4 режимах.
FEAL –Fast Data Encipherment Algorithm (быстрый алгоритм шифрования)	Предложен 1987 г. как альтернатива DES	Ориентирован на 8 разрядный процессор; длина ключа 64 бита
IDEA –International Data Encryption Algorithm (международный алгоритм шифрования)	Предложен в 1991 г.	64- битные блоки открытого текста последовательно шифруются на 128 битном ключе, 8 проходов
ГОСТ 28147-89	Отечественныйалгоритм блочного шифрования. Разработан в середине 80-х годов в СССР.	Предусматривает 3 режима шифрования: простой замены, гаммирования и гаммирования с обратной связью; размер блока 64 бита, длина ключа 256 бит.
RC5 (Rivest Cipher -5)	Быстрый алгоритм блочного шифрования, предложен Роном Ривестом в 1994 г.	Параметризованный алгоритм с переменной длиной блока, переменным размером ключа и переменным числом циклов; блок может иметь длину 32, 64 или 128 бит; число циклов варьируется от 0 до 255, размер ключа - от 0 до 255 бит.
AES (Advanced Encryption Standard)	Предложен Vincent Rijmen и Joan Daemen, начальные буквы фамилий которых и образуют название алгоритма – Rijndael, который является основой алгоритма AES в 2000 г.	Шифр имеет переменную длину блоков и различные длины ключей. Длина ключа и длина блока могут быть выбраны независимо друг от друга 128, 192 и 256 битам.

3.8. Асимметричные криптосистемы

Симметричные криптосистемы, несмотря на множество преимуществ, обладают одним серьезным недостатком. Он связан с ситуацией, когда общение между собой производят не три-четыре человека, а десятки, сотни и даже тысячи людей. В этом случае для каждой пары, переписывающейся между собой, необходимо создавать свой секретный симметричный ключ. Это в итоге приводит к существованию в системе из N пользователей N²/2 ключей. Кроме того, при нарушении конфиденциальности какой-либо рабочей станции, злоумышленник получает доступ ко всем ключам этого пользователя и может отправлять, якобы от его имени, сообщения всем абонентам, с которыми «жертва» вела переписку.

Своеобразным решением этой проблемы явилось появление асимметричной криптографии. Эта область криптографии очень молода, но очень активно развивается. Первая схема, имевшая прикладную значимость, была предложена всего около 20 лет назад. Но за это время асимметричная криптография превратилась в одно из основных направлений криптологии, и используется в современном мире также часто, как и симметричные схемы.

Асимметричная криптография изначально задумана как средство передачи сообщений от одного объекта к другому (а не для конфиденциального хранения информации, которое обеспечивают только симметричные алгоритмы).

Основой асимметричной криптосистемы является асимметричный алгоритм шифрования. В алгоритмах с открытым ключом (также называемых асимметричными) для шифрования и дешифрования используются различные ключи, причем должно быть соблюдено следующее требование: вычисление ключа дешифрования по ключу шифрования должно быть практически невыполнимо. Кроме того, свойство необратимости процедуры шифрования говорит о том, что даже при известном ключе шифрования и наличии зашифрованного текста восстановить исходное сообщение не представляется возможности.

При использовании таких алгоритмов ключ шифрования может быть опубликован для всеобщего пользования, то есть быть открытым, так как зная его все равно невозможно прочесть сообщение. Любой человек, желающий послать шифрованное сообщение, может воспользоваться открытым ключом, однако дешифровать сообщение сможет только человек, знающий ключ дешифрования, который называется закрытым ключом.

Операция шифрования и дешифрования алгоритмом с открытым ключом K обозначается так же, как в случае симметричного алгоритма:

Е_К1 (О) = С,

D_К2 (С) = О.

Ясно, что в отличие от симметричных алгоритмов при использовании алгоритмов с открытым ключом не возникает проблемы передачи ключа. В таких системах для шифрования данных используется один ключ, а для расшифрования – другой. Разумеется, ключ дешифрования не может быть определен из ключа шифрования.

В целом, система переписки при использовании асимметричного шифрования выглядит следующим образом. Для каждого из N абонентов, ведущих переписку, выбрана своя пара ключей: открытый K1 _j и закрытый K2 _j, где j – номер абонента. Все открытые ключи известны всем пользователям сети, каждый закрытый ключ, наоборот, хранится только у того абонента, которому он принадлежит. В случае если абонент под номером 3 собирается передать информацию абоненту номер 9, он шифрует данные открытым ключом шифрования K1 ₉ и отправляет ее 9-му абоненту, который сможет дешифровать сообщение своим секретным ключом K2 ₉. Другие абоненты, имеющие в наличии ключ шифрования абонента 9, не смогут, тем не менее, прочесть шифрованное послание 3-го абонента в силу необратимости шифрования по открытому ключу.

Если абонент номер 9 захочет ответить своему собеседнику номер 3, то ему нужно будет зашифровать свое ответное послание открытым ключом 3-го абонента K1 ₃ и отправить его номеру 3. Тот, в свою очередь, выполнит дешифровку ответа от номера 9 своим закрытым ключом K2 ₃. и снова никто из любопытствующих абонентов номер 1, 2, 4, …8, 10… N не сможет прочесть это сообщение.

В асимметричных системах количество существующих ключей связано с количеством абонентов линейно (в системе из N пользователей используется 2* N ключей), а не квадратично, как в симметричных системах. Помимо этого, при нарушении конфиденциальности m -ой рабочей станции злоумышленник узнает только ключ K2 _m: это позволяет ему читать все сообщения, приходящие абоненту m, но не позволяет выдавать себя за него при отправке писем.

Большинство асимметричных алгоритмов основано на необратимых функциях. Все действующие сейчас системы опираются на один из следующих типов необратимых преобразований:

1. разложение больших чисел на простые множители (алгоритм RSA);

2. вычисление логарифма в конечном поле (криптосистема Эль-Гамаля);

3. Вычисление корней алгебраических уравнений на основе эллиптических уравнений ( алгоритм Месси-Омуры).

Дата добавления: 2014-01-15