Криптосистема Эль-Гамаля

Данная система является альтернативой алгоритму RSA и при равном значении ключа обеспечивает ту же криптостойкость. Эль-Гамаль (Taher Elgamal) усовершенствовал алгоритм Диффи-Хеллмана и получил алгоритмы для шифрования и для обеспечения аутентификации. Алгоритм основан на проблеме поиска дискретного логарифма. Если возводить целое число в степень достаточно легко, то восстановить целочисленный аргумент по значению (то есть найти логарифм) довольно трудно.

Для генерации пары ключей сначала выбирается простое число p и два случайных числа, g и x, оба меньше p. Затем вычисляется

y = g^x mod p.

Открытым ключом являются y, g и p. Величины g, и p можно сделать общими для группы пользователей. Закрытым ключом является x.

Для шифрования сообщения M сначала выбирается случайное число k,

взаимно простое с (p – 1). Затем вычисляются

a = g^k mod p,

b = y^k M mod p.

Пара (a, b) является шифротекстом. Получаемый шифротекст в два раза длиннее открытого текста. Для дешифрирования (a, b) вычисляется

M = b / a^x mod p.

Так как a^x ≡ g^kx (mod p) и b/a^x ≡ y^k M/a^x ≡ g^xk M/ g^kx = M (mod p), то все действительно так и получается. Или иначе:

a^x mod p = y^k mod p 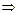(g^k mod p)^x mod p = (g^x mod p) ^k mod p.

Каждая подпись или шифрование алгоритмом ELGamal требует нового значения k, и это значение должно быть выбрано случайным образом. Если когда-нибудь злоумышленник раскроет k, он сможет раскрыть закрытый ключ x. Если злоумышленник когда-нибудь сможет получить два сообщения, подписанные или зашифрованные с помощью одного и того же k, то он сможет раскрыть x, даже не зная значение k.

Рассмотрим алгоритм криптосистемы Эль-Гамаля.

Выбираем открытый ключ p и g:

p простое число (может быть общим для группы пользователей),

g < p (может быть общим для группы пользователей).

Выбираем закрытый ключ x < p.

Вычисляем y =g^x mod p.

Шифрование:

выбираем случайное k, которое взаимно простое с p –1;

a (шифротекст) =g^k mod p,

b (шифротекст)= M (y^k mod p).

Дешифрирование:

M (открытый текст) = b / a^x mod p.

Приведем пример использования метода Эль-Гамаля для шифрования сообщения 2, 5, 7. Для простоты вычислений будем использовать маленькие числа (на практике используются числа существенно большие).

1. Выберем простое число p =19; g= 5 (g < p);

k =13 (взаимно простое с p –1); x =11.

2. Вычисляем y =g^x mod p =5¹¹mod 19=6.

3. Шифруем сообщение a=g^k mod p= 5¹³ mod 19=17,

b₁ = M₁ (y^k mod p)=2 (6¹³ mod 19)=8,

b₂ = M₂ (y^k mod p)=5 (6¹³ mod 19)=20,

b₃ = M₁ (y^k mod p)=7 (6¹³ mod 19)=28.

4. Дешифрование сообщения

M₁ = b₁ /(a^x mod p)=8/(17¹¹mod 19)=8/4=2,

M₂ = b₂ /(a^x mod p)=20/(17¹¹mod 19)=20/4=5,

M₃ = b₃ /(a^x mod p)=28/(17¹¹mod 19)=28/4=7.

Необходимо отметить, что операции возведения в степень больших чисел достаточно трудоемки для современных процессоров, даже если они производятся по оптимизированным по времени алгоритмам. Так быстродействие RSA в тысячу раз ниже, чем у DES или ГОСТ 28147-89. Поэтому обычно весь текст сообщения кодируется обычным блочным шифром (симметричным алгоритмом), намного более быстрым, но с использованием ключа сеанса, а вот сам ключ сеанса шифруется как раз асимметричным алгоритмом с помощью открытого ключа получателя и помещается в начало файла. Такой механизм называют цифровым конвертом.

При использовании симметричной и асимметричной криптографии длины ключей должны выбираться так, чтобы вскрыть любой из компонентов системы было одинаково трудно. Необходимо отметить, что длина открытых ключей существенно больше ключей для симметричных алгоритмов (табл. 6).

Таблица. 6. Длины симметричных и открытых ключей
с аналогичной устойчивостью к вскрытию методом перебора

Длина симметричного ключа, в битах	Длина открытого ключа, в битах

Дата добавления: 2014-01-15