Алгоритмы возведения в степень в конечном поле

В системах с открытым ключом активно используется техника возведения в степень в конечном поле или, как ее еще называют, арифметика

вычетов. Такой подход позволяет избежать ситуации переполнения разрядной сетки при работе с большими числами.

Арифметика вычетов очень похожа на обычную арифметику: она коммутативна, ассоциативна и дистрибутивна. Кроме того, приведение каждого промежуточного результата по модулю n дает тот же результат, как и выполнение всего вычисления с последующим приведением конечного результата по модулю n.

;

;

;

.

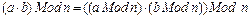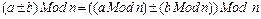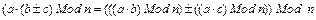Вычисление остатка от деления часто используется в криптографии, так как вычисление дискретных логарифмов и квадратных корней может быть нелегкой проблемой. Арифметика вычетов, к тому же, легче реализуется на компьютерах, поскольку она ограничивает диапазон промежуточных значений и результата. Для k -битовых вычетов n, промежуточные результаты любого сложения, вычитание или умножения будут не длиннее, чем 2 k бит. Поэтому в арифметике вычетов мы можем выполнить возведение в степень без огромных промежуточных результатов. Вычисление степени некоторого числа по модулю другого числа,

a^x mod n,

представляет собой просто последовательность умножений и делений, но существуют приемы, ускоряющие это действие. Один из таких приемов стремится минимизировать количество умножений по модулю, другой - оптимизировать отдельные умножения по модулю. Так как операции дистрибутивны, быстрее выполнить возведение в степень как поток последовательных умножений, каждый раз получая вычеты.

3.13. Сжатие данных

В современном криптоанализе доказано, что вероятность взлома криптосхемы при наличии корреляции между блоками входной информации значительно выше, чем при отсутствии таковой. Основной задачей алгоритмов сжатия данных и является устранение избыточности, то есть корреляций между данными во входном тексте. Все современные криптоалгоритмы перед шифрованием информации производят ее сжатие, что повышает их криптостойкость. Необходимо подчеркнуть, что сжатие идет до шифрования, а не наоборот, так как после шифрования сжимать будет нечего.

Все алгоритмы сжатия данных качественно делятся на алгоритмы сжатия без потерь и с потерями исходной информации. При использовании первых алгоритмов данные восстанавливаются без изменений. Вторые ‑ удаляют из потока данных информацию, незначительно влияющую на их суть, либо вообще не воспринимаемую человеком. Эти алгоритмы широко используются для сжатия аудио- и видеоизображений. В криптосистемах, естественно, используется только первая группа алгоритмов.

Существует ряд методов сжатия без потерь, наиболее известными из них являются:

─ алгоритм Хаффмана (Huffman), ориентированный на сжатие любой последовательности байт, не связанных между собой;

─ алгоритм Лемпеля-Зива (создатели Lempel и Ziv), ориентированный на сжатие текстов, в которых есть неоднократно повторяющиеся «слова» ‑ последовательности байт или бит;

─ алгоритм Уэлча (Welch) как модифицированный алгоритм Лемпеля-Зива ‑ LZW.

Практически все популярные программы архивации без потерь (RAR, ARJ, ZIP) используют эти методы.

Алгоритм Хаффмана

Кодирование Хаффмана основывается на предпосылке, что некоторые символы используются в представлении данных чаще, чем другие. Наиболее общее представление – алфавит ASCII – использует 8 бит для каждого символа. В английском языке буква ‘a’ чаще встречается, чем буква ‘q’, а в русском – буква ‘и’ чаще чем ‘ж’ хотя мы используем для их представления одинаковое количество бит. Если мы, например, используем только 4 бита для кодирования буквы ‘и’ и 12 бит для ‘ж’, то исходный русский текст можно записать меньшим число бит без потери информации.

Кодирование Хаффмана использует идею связи длины символа с вероятностью появления символов. Статическое кодирование Хаффмана требует, чтобы таблица вероятностей была известной, прежде чем начать сжимать данные. Эта таблица может быть взята из результатов статистических исследований, или система сжатия может просканировать входные данные для определения вероятностей символов, прежде чем начать сжимать данные.

С помощью этой информации о вероятностях компрессор и декомпрессор могут сконструировать кодирующее дерево. Это двоичное дерево с одним листом для каждого символа. Построение дерева компрессором начинается с двух символов, имеющих наименьшую вероятность. Эти листы помещаются на одну ветку, которой назначается сумма вероятностей. Компрессор затем рассматривает эту ветку вместе с оставшимися символами в списке вероятностей, и снова выбирает два наименее вероятных элемента. Он продолжает строить и объединять ветки, пока не получит единое дерево с вероятностью корня, равной 1.

Полученное дерево имеет листья с различным расстоянием от корня. Листья, которые представляют символы с наивысшей вероятностью, самые близкие к корню, тогда как символы с наименьшей вероятностью находятся дальше от корня. Для кодировки символа записывается путь от корня дерева к листу, где располагается этот символ, причем каждая ветка кодируется 0 или 1.

В качестве примера рассмотрим кодирование следующей строки

EDDBAABCDDDEEFDE.

Таблица вероятностей для каждого символа:

A=2/16; B=2/16; C=1/16; D=6/16; E=4/16; F=1/16.

На рис. 9 показано бинарное кодирующее дерево. На основании его таблица кодировки символов выглядит следующим образом:

D – 00; E – 01; B – 100; A – 101; F – 111; C – 110.

Если до сжатия для кодировки каждого символа использовалось 3 бита (для всего сообщения – 16*3=48 бит), то при кодировании Хаффмана требуется на 10 бит меньше (для всего сообщения – 38 бит).

Алгоритм Лемпеля-Зива

Алгоритм LZ77 (опубликован в 1977 г) формулируется следующим образом: «если в прошедшем ранее выходном потоке уже встречалась подобная последовательность байт, причем запись о ее длине и смещении от текущей позиции короче, чем сама эта последовательность, то в выходной файл записывается ссылка (смещение, длина), а не сама последовательность».

Например, фраза:

КОЛОКОЛ_ОКОЛО_КОЛОКОЛЬНИ

Закодируется как:

КОЛО(-4,3)_(-5,4)О_(-14,7)ЬНИ

Подклассом данного алгоритма является широко распространенный метод сжатия RLE (Run Length Encoding), который заключается в записи вместо последовательности одинаковых символов одного символа и их количества. Последовательность AAAAAABBBBB с помощью алгоритма RLE будет закодирована как (A, 6) (B, 5).

Рис. 9. Бинарное дерево при статическом кодировании Хаффмана

Алгоритм LZW

Этот алгоритм расширяет алфавит, для этого он использует дополнительные символы для представления строк обычных символов. При использовании LZW-сжатия восьмибитовых кодов ASCII алфавит расширяется с использованием девяти и больших битовых кодов. Дополнительные 256 кодов, которые появляются при 9-битовом коде, используются для хранения строк 8-битовых кодов, которые определяются из строк во входном потоке.

Алгоритм сжатия работает следующим образом. Начинаем с нулевой строки. Читаем символ и добавляем его к строке. Если строка уже находится в таблице, то продолжаем чтение, пока не получим строку, которой нет в таблице. Добавляем ее к таблице строк. Записываем код для последней известной строки, которая соответствует выходу. Используем последний символ в качестве основы для новой строки, и продолжаем чтение, пока не исчерпаем все входные данные.

3.14. Криптоанализ и защита информации

Криптоанализ – это наука о дешифровке закодированных сообщений не зная ключей.

Рассмотрим существующие криптоаналитические методы вскрытия зашифрованных сообщений. Предположим, что у криптоаналитиков имеется неограниченный доступ к линии связи между отправителем и получателем. В их руках – множество сообщений, переданных по линии связи в шифрованном виде. Задача криптоаналитика состоит в том, чтобы восстановить либо открытый текст, либо ключ. Для решения этой задачи криптоаналитик должен выявить слабые места в криптосистеме, использованной для шифрования данных. В криптографии делается допущение, что криптоаналитик знает полное описание криптографического алгоритма, и секретность сообщения полностью определяется ключом. В таком случае криптоаналитику доступны следующие методы вскрытия:

1. Вскрытие на основе только шифротекста (ciphertext-only attack). Это ситуация, когда атакующий не знает ничего о содержании сообщения, и ему приходится работать лишь с самим шифрованным текстом. На практике часто имеется возможность сделать правдоподобные предположения о структуре текста, поскольку многие сообщения имеют стандартные заголовки. Также часто можно предположить, что некоторый блок информации содержит заданное слово. Опираясь на шифротексты нескольких сообщений, зашифрованных одним и тем же алгоритмом, криптоаналитик должен восстановить открытый текст как можно большего числа шифрованных сообщений или выявить ключи шифрования.

2. Вскрытие на основе открытого текста (known-plaintext attack). Криптоаналитик должен вскрыть текст как можно большего числа зашифрованных сообщений или выявить ключи шифрования, используя несколько открытых текстов и их шифротексты.

3. Вскрытие методом избранного открытого текста (chosen-plaintext attack). В этом случае в дополнение к предыдущему методу криптоаналитик имеет возможность подбора открытого текста для последующего шифрования, поэтому его задача расширяется – он должен раскрыть ключи шифрования сообщений. Некоторые методы шифрования, в частности RSA, весьма уязвимы для атак этого типа.

4. Вскрытие на основе адаптивного выбора открытого текста. В этом методе криптоаналитик также может шифровать открытый текст и, в дополнение к предыдущему методу, по ходу работы уточнять свой последующий выбор открытого текста, опираясь на достигнутые результаты взлома.

5. Вскрытие с использованием избранного шифротекста. Криптоаналитик имеет возможность подбирать различные шифротексты для последующего дешифрования и в его распоряжении имеется несколько дешифрованных открытых текстов. Его задача состоит в раскрытии ключей дешифрования.

6. Вскрытие с использованием избранного ключа. В этом случае криптоаналитик располагает некоторыми сведениями о ключах шифрования, используя их для вскрытия ключа.

7. Атака-«подстава» (Man-in-the-middle attack). Атака направлена на обмен шифрованными сообщениями на протокол обмена ключами. Идея заключается в том, что когда две стороны обмениваются ключами для секретной коммуникации, Злоумышленник внедряется между ними на линии обмена сообщениями и выдает каждой стороне свои ключи. В результате каждая из сторон будет иметь разные ключи, каждый из которых известен Злоумышленнику. Он будет расшифровывать каждое сообщение своим ключом и затем зашифровывать его с помощью другого ключа перед отправкой адресату. Стороны будут иметь иллюзию секретной переписки, в то время как на самом деле Злоумышленник полностью контролирует все сообщения.

8. Атака с помощью таймера (timing attack). Этот тип атак основан на последовательном измерении интервалов времени, затрачиваемых на выполнение операций возведения в степень по модулю целого числа. Этой атаке подвержены по крайней мере следующие шифры: RSA, Диффи-Хеллман и метод эллиптических кривых.

9. Бандитский криптоанализ. Получение ключа производится путем шантажа, угроз, пыток, подкупа и т.д. Это самый эффективный вид криптоанализа.

Способность криптосистемы противостоять атакам (активного или пассивного) криптоаналитика называется стойкостью. Количественно стойкость измеряется как сложность наилучшего алгоритма, приводящего к успеху с приемлемой вероятностью. В зависимости от целей и возможностей криптоаналитика меняется и стойкость. Различают:

· Стойкость ключа (сложность раскрытия ключа наилучшим известным алгоритмом);

· Стойкость бесключевого чтения;

· Имитостойкость (сложность навязывания ложной информации наилучшим известным алгоритмом);

· Вероятность навязывания ложной информации.

Это иногда совершенно различные понятия, не связанные между собой. Некоторые криптосистемы, например RSA, позволяют навязывать ложную информацию со сложностью, практически не зависящей от стойкости ключа. Аналогично можно различать стойкость собственно криптоалгоритма, стойкость протокола, стойкость алгоритма генерации и распространения ключей.

Уровень стойкости зависит от возможностей криптоаналитика и от пользователя. Так, различают криптоанализ на основе только шифрованного текста, когда криптоаналитик располагает только набором шифрограмм и не знает открытых текстов, и криптоанализ на основе открытого текста, когда криптоаналитик знает открытые и соответствующие шифрованные тексты.

Так как криптоалгоритм обычно должен быть достаточно универсальным, естественным представляется требование, чтобы стойкость ключа не зависела от распределения вероятностей источника сообщений. В общем случае источник сообщений может вырабатывать «удобные» для нарушителя сообщения, которые могут стать ему известными. В этом случае говорят о криптоанализе на основе специально выбранных открытых текстов. Очевидно, что стойкость ключа по отношению к анализу на основе выбранных текстов не может превышать стойкости по отношению к анализу на основе открытых текстов, а она, в свою очередь, не может превышать стойкости по отношению к анализу на основе шифрованных текстов. Иногда разработчиками СЗИ допускается даже, что враждебный криптоаналитик может иметь доступ к криптосистеме, то есть быть «своим».

Обычно криптоалгоритмы разрабатывают так, чтобы они были стойкими по отношению к криптоанализу на основе специально выбранных открытых текстов.

Понятие «наилучшего алгоритма» раскрытия ключа в определении стойкости неконструктивно и допускает субъективное толкование (для кого-то из разработчиков).

Для взлома криптосистем в настоящее время применяются вычислительные средства. Скорость вскрытия приблизительно определяется максимальной оценкой, подсчитанной согласно каждому из следующих параметров:

· по объему исходных данных, необходимых для вскрытия;

· по количеству процессорного времени, необходимого для вскрытия;

· по объему памяти компьютера, необходимой для вскрытия;

Эти величины подсчитываются приблизительно, с указанием порядка величин. Например, если для вскрытия алгоритма необходимо выполнить 2¹²⁸ операций (часто встречающееся значение), значит, при быстродействии компьютера миллиард операций в секунду, ему потребуется примерно 10¹⁹ лет, чтобы расшифровать текст, что значительно превышает время жизни Вселенной.

Надежность алгоритмов криптографии основана на неприемлемой трудоемкости их взлома. Если взлом алгоритма (даже «лобовым» методом, т.е. получив образец шифротекста и выполняя его дешифрование перебором возможных ключей проверять осмысленность полученного текста) обойдется дороже, чем ценность зашифрованной информации, или время, потраченное на его взлом, превосходит срок секретности данных, можно считать ситуацию относительно безопасной.

3.15. Стеганография

Стеганография – это метод организации связи, который собственно скрывает само наличие связи. В отличие от криптографии, где злоумышленник точно может определить является ли передаваемое сообщение зашифрованным текстом, методы стеганографии позволяют встраивать секретные сообщения в безобидные послания так, чтобы невозможно было заподозрить существование встроенного тайного послания.

Слово «стеганография» в переводе с греческого буквально означает «тайнопись» (steganos – секрет, тайна; graphy – запись). К ней относится огромное множество секретных средств связи, таких как невидимые чернила, микрофотоснимки, условное расположение знаков, тайные каналы и средства связи на плавающих частотах и т. д.

Стеганография занимает свою нишу в обеспечении безопасности: она не заменяет, а дополняет криптографию. Сокрытие сообщения методами стеганографии значительно снижает вероятность обнаружения самого факта передачи сообщения. А если это сообщение к тому же зашифровано, то оно имеет еще один, дополнительный, уровень защиты.

В настоящее время в связи с бурным развитием вычислительной техники и новых каналов передачи информации появились новые стеганографические методы, в основе которых лежат особенности представления информации в компьютерных файлах, вычислительных сетях и т. п. Это дает возможность говорить о становлении нового направления – компьютерной стеганографии.

Несмотря на то, что стеганография как способ сокрытия секретных данных известна уже на протяжении тысячелетий, компьютерная стеганография ‑ молодое и развивающееся направление.

Как и любое новое направление, компьютерная стеганография долгое время не имела единой терминологии. В 1996 году на конференции Information Hiding: First Information Workshop было предложено использовать единую терминологию и обговорены основные термины.

Стеганографическая система или стегосистема – совокупность средств и методов, которые используются для формирования скрытого канала передачи информации.

При построении стегосистемы должны учитываться следующие положения:

· Злоумышленник имеет полное представление о стеганографической системе и деталях ее реализации. Единственной информацией, которая остается неизвестной потенциальному противнику, является ключ, с помощью которого только его держатель может установить факт присутствия и содержание скрытого сообщения.

· Если злоумышленник каким-то образом узнает о факте существования скрытого сообщения, это не должно позволить ему извлечь подобные сообщения в других данных до тех пор, пока ключ хранится в тайне.

· Потенциальный злоумышленник должен быть лишен каких-либо технических и иных преимуществ в распознавании или раскрытии содержания тайных сообщений.

Обобщенная модель стегосистемы представлена на рис. 10.

Рис. 10. Модель передачи данных с использованием стегосистемы

В качестве данных может использоваться любая информация: текст, сообщение, изображение и т. п. В общем же случае сообщением может быть как текст или изображение, так и, например, аудиоданные. Далее для обозначения скрываемой информации, будем использовать именно термин «сообщение».

Контейнер – любая информация, предназначенная для сокрытия тайных сообщений.

Пустой контейнер - контейнер без встроенного сообщения; заполненный контейнер или стего - контейнер, содержащий встроенную информацию.

Встроенное (скрытое) сообщение – сообщение, встраиваемое в контейнер.

Стеганографический канал (или просто стегоканал) ‑ канал передачи стего.

Стегоключ (или просто ключ) ‑ секретный ключ, необходимый для сокрытия информации. В зависимости от количества уровней защиты (например, встраивание предварительно зашифрованного сообщения) в стегосистеме может быть один или несколько стегоключей.

По аналогии с криптографией, по типу стегоключа все стегосистемы можно подразделить на два типа: с секретным ключом и с открытым ключом.

В стегосистеме с секретным ключом используется один ключ, который должен быть определен либо до начала обмена секретными сообщениями, либо передан по защищенному каналу.

В стегосистеме с открытым ключом для встраивания и извлечения сообщения используются разные ключи, которые различаются таким образом, что с помощью вычислений невозможно вывести один ключ из другого. Поэтому один ключ (открытый) может передаваться свободно по незащищенному каналу связи. Кроме того, данная схема хорошо работает и при взаимном недоверии отправителя и получателя.

Дата добавления: 2014-01-15