
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод наименьших квадратов. Технология регрессионного анализа
|
|
|
|
Технология регрессионного анализа.
Метод наименьших квадратов (МНК) используется для представления.в виде формулы данных, заданных таблично.
Таблица 1
| x | x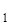
| x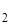
| ... | x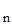
|
| f(x) | y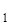
| y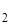
| ... | y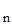
|
Приближение по МНК формулируется следующим образом:
Для функции f(x), заданной табл. 1, найти приближающую функцию F(x) так, чтобы сумма квадратов
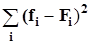 = min,
= min,
где f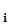 и F
и F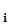 - значения функции f(x) и приближающей функции F(x) при одних и тех же значениях х
- значения функции f(x) и приближающей функции F(x) при одних и тех же значениях х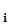 .
.
Разность функций берётся в квадрате, чтобы её знак был всегда положительным.
 |

 f(x),
f(x),


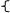
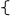

 F(x) f(x) F(x)
F(x) f(x) F(x)
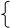

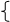





 | |||||
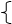 |  | ||||
 | |||||
 х
х
Рис. 1 Точки функции f(x) из таблицы и приближающая функция F(x)
В качестве приближающих функций F(x) в зависимости от характера точечного графика (рис.1.) используются следующие основные функции:
1. F(x) = ах+b, 2. F(x) = ax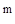 +bx+c, 3. F(x) =
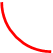
+bx+c, 3. F(x) = 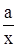 + b,
+ b,
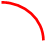


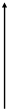
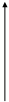





 параметры а, b параметры a, b, c, m параметры а, b
параметры а, b параметры a, b, c, m параметры а, b
4. F(x) = a e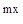 , 5. F(x) = a lnx + b
, 5. F(x) = a lnx + b
параметры a, m параметры а, b


 и другие функции.
и другие функции.

 a
a
Для приближающей функции с 2-мя параметрами F(x,a,b) сумма квадратов разностей f(x) и F(x) имеет вид:
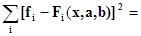 Ф(a,b),
Ф(a,b),
условие минимума примет вид системы уравнений частных производных по параметрам a, b:
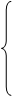
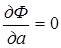 ;
;
(4)  ;
;
то есть
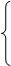
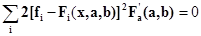
(5) 
Коэффициент 2 не равен 0, поэтому его можно убрать из системы уравнений (5).
Пример. Определить зависимость F=F(Х) для данных, заданных таблицей 2:
Таблица 2
| Х, шт. | |||||||||
| F, $ | 8,67 | 5,33 | 4,86 | 4,5 | 4,22 |
Точечный график,построенный по табл. 2, показывает, что приближающей функцией для него является зависимость под номером №3:
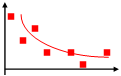 F(x) =
F(x) = 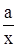 + b C
+ b C
Нужно определить параметры a и b.
q
Согласно (5)
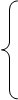
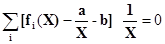
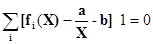
или
 (22 -
(22 -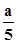 - b)
- b)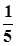 + (12 -
+ (12 - 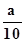 - b)
- b) 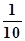 +(8,67 -
+(8,67 -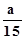 - b)
- b) 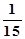 +...
+...
+(4,22 -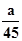 -b)
-b)  =0;
=0;
(22 -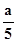 - b) 1 + (12 -
- b) 1 + (12 - 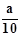 - b) 1+(8,67 -
- b) 1+(8,67 -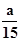 - b) 1+...
- b) 1+...
+(4,22 - 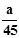 -b) 1=0
-b) 1=0
Получили систему из двух уравнений с двумя неизвестными. После раскрытия скобок, преобразований и решения этой системы уравнений получим, что коэффициент а = 100, коэффициент b = 2
т.е. F(X) = 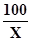 + 2,
+ 2,
т.е. таблицу 2 можно заменить этим уравнением.
Полученное уравнение является уравнением регрессии или линией тренда, которая показывает тенденцию изменения функции
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 357; Нарушение авторских прав?; Мы поможем в написании вашей работы!