Учебные вопросы

Общая процедура идентификации одномерного временного ряда на основе методологии Бокса-Дженкинса.

Метод Гуйарати для оценки влияния структурных изменений на динамику изучаемого показателя.

Тест Чоу для оценки влияния структурных изменений на динамику изучаемого показателя.

Изменение характера тенденции временного ряда.

ПЛАН

Москва

КОНСПЕКТ ЛЕКЦИИ № 6

на тему: Моделирование тенденции временного ряда при наличии структурных изменений

Дисциплина: Эконометрика

1. Изменение характера тенденции временного ряда.

От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными факторами. В этом случае, начиная с некоторого момента времени t*, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику.

Рис. 1. Изменение характера тенденции временного ряда

Момент времени t* сопровождается значительными изменениями ряда факторов, оказывающих сильное воздействие на изучаемый показатель y_t. Чаще всего эти изменения вызваны изменениями в общеэкономической ситуации или факторами глобального характера, приведшими к изменению структуры экономики. Если исследуемый временной ряд включает в себя соответствующий момент времени, то одной из задач его изучения становится выяснение вопроса о том, значимо ли повлияли общие структурные изменения на характер этой тенденции.

Если это влияние значимо, то для моделирования тенденции данного временного ряда следует использовать кусочно-линейные модели регрессии, т.е. разделить исходную совокупность на две подсовокупности (до момента t* и после момента t*) и построить отдельно по каждой подсовокупности уравнения линейной регрессии:

y⁽¹⁾ = a₁ + b₁t;

y⁽²⁾ = a₂ + b₂t.

Если структурные изменения незначительно повлияли на характер тенденции ряда у_t, то ее можно описать с помощью единого уравнения тренда для всей совокупности данных:

y⁽³⁾ = a₃ + b₃t.

Каждый из описанных выше подходов имеет свои положительные и отрицательные стороны. При построении кусочно-линейной модели происходит снижение остаточной суммы квадратов по сравнению с единым для всей совокупности уравнением тренда. Однако разделение исходной совокупности на две части ведет к потере числа наблюдений и, следовательно, к снижению числа степеней свободы в каждом уравнении кусочно-линейной модели. Построение единого для всей совокупности уравнения тренда, напротив, позволяет сохранить число наблюдений n исходной совокупности, однако остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной моделью. Очевидно. что выбор одной из двух моделей будет зависеть от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.

2. Формальный статистический тест для оценки этого соотношения был предложен Грегори Чоу. Применение этого теста предполагает расчет параметров уравнений трендов для всех кусков прямых и единой прямой.

Введем систему обозначений.

n₁ и n₂ – число наблюдений по кусочно-линейной модели;

n – число наблюдений по всей совокупности;

С¹_ост и С²_ост – остаточная сумма квадратов по кусочно-линейной модели;

С³_ост – остаточная сумма квадратов по всей совокупности;

k₁ и k₂ – число параметров в кусочно-линейном уравнении;

k₃ – число параметров в едином уравнении;

n₁ – k₁ и n₂ – k₂ – число степеней свободы остаточной дисперсии в кусочно-линейном уравнении;

n – k₃ = (n₁ + n₂) – k₃ - число степеней свободы остаточной дисперсии в едином уравнении тренда.

Выдвинем гипотезу Н₀ о структурной стабильности тенденции изучаемого временного ряда.

Остаточную сумму квадратов по кусочно-линейной модели (С^кл_ост) можно найти как сумму С¹_ост и С²_ост:

С^кл_ост = С¹_ост + С²_ост (1)

Соответствующее ей число степеней свободы составит:

(n₁ – k₁) + (n₂ – k₂) = (n – k₁ – k₂). (2)

Тогда сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели можно определить следующим образом:

ΔС_ост = С³_ост – С^кл_ост. (3)

Число степеней свободы, соответствующее ΔС_ост, с учетом соотношения (2) будет равно

n – k₃ – (n – k₁ – k₂) = k₁ + k₂ – k₃. (4)

Далее определяется фактическое значение F - критерия по следующим дисперсиям на одну степень свободы вариации:

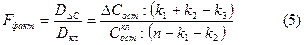
Найденное значение F_факт сравнивают с табличным, полученным по таблицам распределения Фишера для уровня значимости α и числа степеней свободы (k₁ + k₂ – k₃) и (n – k₁ – k₂).

Если F_факт > F_табл, то гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных изменений на динамику изучаемого показателя признают значимым. В этом случае моделирование тенденции временного ряда следует осуществлять с помощью кусочно-линейной модели. Если F_факт < F_табл, то нет оснований отклонять ноль-гипотезу о структурной стабильности тенденции. Ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения тренда.

Дата добавления: 2014-01-15