Интегрирование

6.1. Неопределённый интеграл. Первообразная и неопределённый интеграл функции. Линейность неопределённого интеграла. Замена переменной и интегрирование по частям. Интегрирование рациональных и рационально-тригонометрических функций.

6.2. Определённый интеграл. Разбиение отрезка. Понятия интегрируемой по Риману функции и интеграла Римана. Ограниченность интегрируемой по Риману функции. Интегральные суммы Дарбу, верхний и нижний интегралы и их связь с интегралом Римана. Колебание функции на множестве. Необходимый и достаточный признак интегрируемости функции по Риману. Интегрируемость непрерывной функции. Теорема об интегрируемости функции, имеющей конечное число разрывов. Интегрируемость монотонной ограниченной функции. Линейность, аддитивность и монотонность интеграла Римана. Теоремы об интегрируемости модуля и произведения интегрируемых функций. Первая и вторая теоремы о среднем.

Связь определённого интеграла с первообразной. Формула Ньютона – Лейбница. Интегрирование по частям и замена переменной в определённом интеграле. Формула Тейлора с остаточным членом в интегральной форме.

6.3 Несобственные интегралы. Два типа несобственных интегралов. Понятие сходимости несобственного интеграла, абсолютная и условная сходимости. Главное значение несобственного интеграла. Формулы интегрирования по частям и замены переменной в несобственном интеграле. Признаки сходимости несобственных интегралов: признак сравнения, критерий Коши, признаки Абеля и Дирихле. Интегральный признак сходимости рядов.

7. Пространство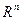

7.1. Пространство 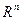. Понятие метрики. Метрическая структура в 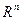. Евклидова метрика. Линейная (векторная) и евклидова структуры в 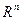. Норма и скалярное произведение векторов. Неравенство Коши – Буняковского. Стандартный базис в 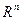. Евклидова и другие нормы.

Открытые и замкнутые шары. Открытые и замкнутые множества. Внутренние и внешние точки множества. Граница множества. Теоремы об объединениях и пересечениях для систем открытых и замкнутых множеств. Понятие окрестности точки и множества. Предельные точки множества. Замыкание множества. Теорема о том, что замыкание множества есть наименьшее замкнутое множество, его содержащее. Понятие открытого покрытия множества. Компактные множества. Лемма о вложенных замкнутых кубах. Теорема о компактности замкнутого куба. Теорема Гейне – Бореля.

Сходимость последовательностей точек в 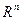. Единственность предельной точки сходящейся последовательности. Теорема о существовании сходящейся подпоследовательности ограниченной последовательности точек. Критерий Коши.

7.2. Функции многих переменных. Функции из 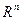в 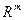(вектор-функции). Предел функции в точке. Единственность предела. Понятия ограниченной функции и колебания функции на множестве. Критерий Коши существования предела функции в точке.

Непрерывность функции в точке (определения через окрестности и через предел). Теорема о локальной ограниченности функции, непрерывной в точке. Теорема о локальной положительности скалярной функции, непрерывной и положительной в точке. Непрерывность в точке суммы, произведения, частного и композиции двух функций.

Непрерывность функции на множестве. Теорема об открытости прообраза открытого множества при непрерывном отображении. Теорема о компактности образа компактного множества. Понятие равномерной непрерывности. Теорема о равномерной непрерывности функции, непрерывной на компакте. Теорема о максимальном и минимальном значении непрерывной функции, заданной на компакте. Эквивалентность норм в .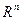

Понятие пути в 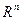. Линейно связные множества. Понятие области. Теорема о промежуточном значении скалярной функции, заданной на области.

8. Основы дифференциального исчисления в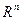

8.1. Производная функции многих переменных. Линейные отображения, их непрерывность и норма. Матрица линейного отображения. Дифференцируемость функции и её дифференциал (производная). Единственность дифференциала (корректность его определения). Дифференциал суммы, произведения, частного и композиции двух функций. Дифференциал обратной функции. Теорема о конечном приращении скалярной функции многих переменных. Теорема о постоянстве функции на области, где её дифференциал равен нулю.

8.2. Частные производные. Производная функции по направлению и её представление в виде предела. Частные производные. Координатное представление дифференциала отображения. Матрица Якоби. Матрица Якоби обратной функции. Достаточное условие дифференцируемости отображения (через частные производные). Градиент скалярной функции и его представление в декартовых координатах. Простейшие свойства градиента. Дивергенция и ротор вектор-функций. Их механический смысл.

8.3. Производные высших порядков. Производная по направлению порядка выше единицы. Частные производные высших порядков. Перестановочность частных производных. Формула Тейлора. Понятие дифференциала (производной) высшего порядка. Симметричность второго дифференциала.

8.4. Экстремум функции многих переменных. Понятие экстремума функции. Стационарная (критическая) точка функции. Необходимое условие экстремума. Достаточное условие экстремума.

Литература

1. Зорич В. А. Математический анализ. М.: ФАЗИС, 1997. Ч. 1.
2. Решетняк Ю. Г. Курс математического анализа. Новосибирск: Изд-во Ин-та математики, 1999. Ч. 1, Кн.1 – 2.
3. Рудин У. Основы математического анализа. М.: Мир, 1976.
4. Никольский С.М. Курс математического анализа. М.: Наука, 1990. Т. 1.
5. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. М.: Физматлит, 2006. Т. 1 – 2.
6. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1977.
7. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу. М.: ФИЗМАТЛИТ, 2003. Т.1,2,3.

Дата добавления: 2014-01-15