Механическая выборка

Вопрос 3. Способы отбора в выборочную совокупность

Основными способами отбора в выборочную совокупность являются:

1. Собственно случайный отбор (метод жеребьевки или метод лото)

Каждой единице совокупности присваивается порядковый номер, наносимый на определенные предметы (жетоны, фишки, кубики, бочонки, шары, билеты или бумажки), которые затем перемешиваются и выбираются наугад. Владельцы каждого номера имеют одинаковую возможность на выигрыш.

Собственно случайная выборка может быть повторной и бесповторной.

Несмотря на простоту реализации, применяется редко, т.к. уступает другим способам отбора с точки зрения репрезентативности и точности результатов, удобства организации.

Средняя ошибка выборки для выборочной средней и выборочной доли при повторном отборе исчисляется по формулам (7.2), (7.3), при бесповторном отборе – (7.4), (7.5).

Механическая выборка применяется в тех случаях, когда генеральная совокупность каким-либо образом упорядочена или ранжирована, т.е. имеется определенная последовательность в расположении единиц.

Первоначально определяется, какое число единиц необходимо отобрать в выборочную совокупность. Затем разбивают генеральную совокупность на полученное число групп и из каждой группы выбирают по одной единице, стоящей в середине группы. Это позволяет избежать систематической ошибки выборки.

Механический отбор всегда бесповторный.

Пример. Численность студентов второго курса факультета составляет 300 человек. Решено организовать 5%-ное выборочное исследование успеваемости студентов по дисциплине «Статистика» методом механического отбора.

Первоначально ранжируют студентов по баллам, полученным на тести­ровании по дисциплине. Затем делят студентов на 15 групп по числу единиц наблюдения (300´0,05=15 чел.). Из каждой группы выбирают 7-го по порядку студента, т.к. он находится в центре группы. Исследуют успеваемость пятнадцати вошедших в выборку студентов и формулируют вывод относительно успеваемости всех студентов второго курса факультета с определенной погрешностью (ошибкой выборки).

Теоретически средняя ошибка выборки для выборочной средней[4] определяется по формуле:

, (7.6)

где 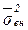– средняя из внутригупповых дисперсий.

Важно! Если генеральная совокупность разбита на группы по строго нейтральному признаку в отношении изучаемого показателя (например, студенты ранжированы по алфавиту, что никак не сказывается на их успеваемости по дисциплине «Статистика»), то средняя из внутригрупповых дисперсий () равна дисперсии общей (). В этом случае при механическом отборе следует применять те же формулы ошибки выборки, что и при собственно случайном бесповторном отборе (7.4), (7.5).

Дата добавления: 2014-01-15