Метод скользящей средней

Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.

Шаг скольжения примем равным трем уровням. Это значит, что скользящее среднее арифметическое значение будет равно:

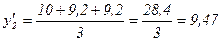тыс. руб./чел. (графа 5 таблицы 9.3).

Таблица 9.3.

Расчет трехзвеньевых скользящих средних

Год	Кварталы     tj	Уровни ряда (средняя выработка рабочих), тыс. руб./ чел. yj	Скользящие суммы (шаг скольжения равен 3), тыс. руб./ чел.	Скользящие трехзвеньевые средние, тыс. руб./ чел.
		10,0	–	–
	9,2	28,4	9,47
	9,2	27,4	9,13
	9,0	26,7	8,90
		8,5	25,5	8,50
	8,0	24,8	8,27
	8,3	24,7	8,23
	8,4	25,5	8,50
		8,8	25,2	8,40
	8,0	27,8	9,27
	11,0	31,0	10,33
	12,0	–	–

Второе оно потому, что записывается в центр принятого шага скольжения, т.е. из трех строк, включенных в расчет, среднее значение записывается в центральную – вторую – строку.

Далее первая строка со значением выработки 10,0 тыс. руб./чел. исключается из расчетов, а принимается в расчет четвертая строка со значением выработки
9,0 тыс. руб./чел. Тогда среднее будет равно:

тыс. руб./чел.

Аналогично

тыс. руб./чел.;

…

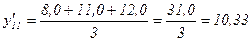тыс. руб./чел.

Поскольку после одиннадцати суммирований принять в расчет по три уровня не удается, то в соответствующих ячейках двенадцатой строки таблицы 9.3 ставятся прочерки.

Согласно данным графы 5 таблицы 9.3, уровни ряда динамики также сначала снижаются, а затем возрастают, как и исходные уровня ряда, однако уже более плавно. Нанесем исходные уровни ряда и скользящие средние на график (рис. 9.2).

Рис. 9.2. Ряд динамики среднеквартальной выработки продукции рабочих предприятия
за три года: фактические и сглаженные уровни ряда

Первого и двенадцатого трехзвеньевого среднего значения на графике нет, поскольку их нет и в таблице 9.3. Это свидетельствует о грамотном построении графика скользящих средних. Пики роста и спада фактических значений выработки сгладились, однако выявить тенденцию ряда по-прежнему не представляется возможным.

2). Метод аналитического выравнивания ряда динамики:

а) по уравнению прямой.

Предположим, что изменение фактических значений выработки можно описать уравнением прямой ,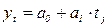

где – значения выровненного ряда, которые нужно вычислить;

а₀, а₁ – параметры уравнения;

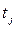– показатели времени (дни, месяцы, годы).

Для расчета коэффициентов a₀, a₁ построим таблицу вспомогательных расчетов 9.4.

Таблица 9.4.

Таблица вспомогательных расчетов для линейного тренда

Год	Кварталы     tj	Уровни ряда (средняя выработка рабочих), тыс. руб./чел. yj	Вспомогательные расчеты
tj ∙ yj		Выровненные значения по уравнению тренда
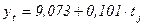
		10,0	10,0		8,65
	9,2	18,4		8,75
	9,2	27,6		8,85
	9,0	36,0		8,95
		8,5	42,5		9,05
	8,0	48,0		9,15
	8,3	58,1		9,25
	8,4	67,2		9,35
		8,8	79,2		9,45
	8,0	80,0		9,55
	11,0	121,0		9,65
	12,0	144,0		9,75
Сумма		110,4	732,0		110,40

Коэффициенты a₀, a₁ определим из системы нормальных уравнений (9.27):

;

.

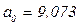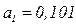Таким образом, уравнение тренда принимает вид: . Подставляя в него поочередно все значения периодов времени t_j (1, 2, 3 … 12), получаем теоретические (выровненные по уравнению прямой) значения выработки продукции (графа 6 таблицы 9.4). Правильность произведенных расчетов подтверждает тот факт, что сумма теоретических уровней ряда равна сумме фактических уровней:

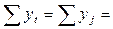110,4 тыс. руб./чел.

Нанесем теоретические значения на рисунок 9.2, построив таким образом рисунок 9.3.

Рис. 9.3. Ряд динамики среднеквартальной выработки продукции рабочих предприятия
за три года: фактические, сглаженные и теоретические уровни ряда

Построенное уравнение динамики необходимо проверить на достоверность с помощью показателя среднеквадратического отклонения теоретических значений выработки от фактических значений:

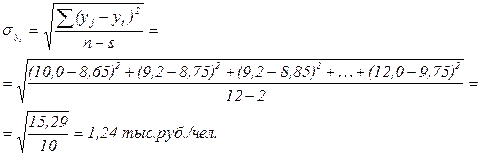
Построим уравнение параболы и сравним полученные значения среднеквадратического отклонения для линейного и параболического трендов.

б) выравнивание ряда динамикипо уравнению параболы.

Параболический тренд имеет вид: 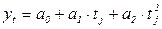, где параметры уравнения параболического тренда находятся по формулам (9.31)-(9.33).

Для упрощения расчетов параметров параболического тренда примем такое обозначение периодов времени , чтобы их сумма была равна нулю (графа 4 таблицы 9.5).

Таблица 9.5.

Таблица вспомогательных расчетов для параболического тренда

Год	Кварталы	Уровни ряда (средняя выработка рабочих), тыс. руб./чел.	Условные обозначения периодов времени	Вспомогательные расчеты
					Выровненные значения по уравнению тренда
		yj	tj	tj ∙ yj
		10,0	-11	-110,0	121,0	1 331	14 641	1 210,0	10,34
	9,2	-9	-82,8	81,0		6 561	745,2	9,51
	9,2	-7	-64,4	49,0		2 401	450,8	8,88
	9,0	-5	-45,0	25,0			225,0	8,43
		8,5	-3	-25,5	9,0			76,5	8,16
	8,0	-1	-8,0	1,0			8,0	8,07
	8,3		8,3	1,0			8,3	8,18
	8,4		25,2	9,0			75,6	8,46
		8,8		44,0	25,0			220,0	8,93
	8,0		56,0	49,0		2 401	392,0	9,58
	11,0		99,0	81,0		6 561	891,0	10,42
	12,0		132,0	121,0	1 331	14 641	1 452,0	11,44
Сумма		110,4		28,8		5 076	48 620	5 754,4	110,40

Коэффициенты a₀, a₁ и 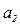определим из системы нормальных уравнений (9.28):

.

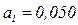
Таким образом, уравнение параболического тренда принимает вид: . Подставляя в него поочередно все значения периодов времени t_j (-11, -7, -7 … 11), получаем теоретические (выровненные по уравнению параболы) значения выработки продукции (графа 10 таблицы 9.5). Правильность произведенных расчетов подтверждает тот факт, что сумма теоретических уровней ряда равна сумме фактических уровней:

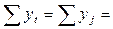110,4 тыс. руб./чел.

Нанесем теоретические значения на рисунок 9.2, построив таким образом рисунок 9.4.

Рис. 9.4. Ряд динамики среднеквартальной выработки продукции рабочих предприятия
за три года: фактические, сглаженные и теоретические уровни ряда

Построенное уравнение динамики необходимо проверить на достоверность с помощью показателя среднеквадратического отклонения:

Вывод: поскольку среднеквадратическое отклонение теоретических значений уровней ряда от фактических значений для параболического тренда составил меньшую величину по сравнению с аналогичным показателем, рассчитанным для линейного тренда (0,66 тыс. руб./чел. < 1,24 тыс. руб./чел.), то для прогнозирования динамики средней выработки на предприятии следует выбрать уравнение параболического тренда.

4. Прогнозирование на основе трендовой модели

Достоверность построенного уравнения параболического тренда позволяет сформулировать прогноз среднеквартальной выработки рабочих предприятия на первое полугодие следующего года. Для этого в качестве периодов времени примем периоды 13, 15, соответствующие первому и второму кварталу следующего года, и подставим данные обозначения в уравнение параболы:

=12,64 тыс. руб./чел.;

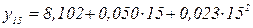=14,03 тыс. руб./чел.

Таким образом, в первом полугодии следующего года прогнозируется рост показателя среднеквартальной выработки рабочих до 12,64 и 14,03 тыс. руб./чел.

5. Оценка сезонной компоненты динамического ряда

Поскольку в п. 3 было доказано наличие тенденции (параболического тренда) в ряду динамики, то расчет индексов сезонности осуществим посредством метода поквартальных отношений:

1 шаг. Теоретические (выровненные по тренду) значения 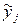, рассчитанные для каждого фактического среднеквартального уровня ряда динамики , приведены в графе 10 таблицы 9.5.

2 шаг. Рассчитаем индексы сезонности по формуле (9.38) и разместим их в графе 5 таблицы 9.6.

Таблица 9.6.

Расчет индексов сезонности

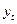
Год	Кварталы     tj	Фактические уровни ряда (выработка одного рабочего), тыс. руб./чел. yj	Теоретические уровни ряда, тыс. руб./чел.	Поквартальные индексы сезонности, %
		10,0	10,34	96,75
	9,2	9,51	96,69
	9,2	8,88	103,62
	9,0	8,43	106,81
		8,5	8,16	104,19
	8,0	8,07	99,08
	8,3	8,18	101,53
	8,4	8,46	99,29
		8,8	8,93	98,55
	8,0	9,58	83,48
	11,0	10,42	105,55
	12,0	11,44	104,86

На основании рассчитанных индексов сезонности построим сезонную волну (рис. 9.5).

Рис. 9.5. Сезонная волна среднеквартальной выработки продукции
рабочих предприятия за три года

Согласно сезонной волне, спады показателя выработки приходятся на второй квартал каждого из трех лет. Подтвердить или опровергнуть данное суждение позволит расчет поквартальных средних индексов сезонности.

3 шаг. Средние за квартал индексы сезонности рассчитаем по формуле (9.34):

- средний индекс сезонности за I квартал:

;

- средний индекс сезонности за II квартал:

;

- средний индекс сезонности за III квартал:

;

- средний индекс сезонности за IV квартал:

.

Таким образом, изучаемое явление подвержено заметной сезонности: спады показателя выработки в расчете на одного рабочего предприятия приходятся на второй квартал каждого из трех анализируемых лет.

Тема 10. Индексный метод анализа

1. Сущность и виды индексов

2. Построение индивидуальных и сводных индексов

3. Изучение динамики явлений при помощи индексов

4. Система индексов динамики средней величины

Дата добавления: 2014-01-15