Solution the system ( 7.1) by method of Jordan-Gauss

The goal of this method is to lead an augmented matrix of system 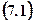to diagonal form. It’s easy to make by using a table.

Table 1. The first 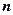columns of the table are columns of the coefficients of the unknowns, next column is a column of constant terms. And the last column (check column) is column whose elements are equal to the sums of elements of each rows.

		…

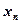
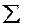
Table 2. (and all subsequent) Consecutively choose diagonal elements distinct from zero. We will call this element a key element and row and column at the intersection of which is the key element, key row and column respectively. Rewrite the key row without changes. All elements of key column we will replace by the rule of rectangular (see §6).

Remark: 1) All zeros rows are deleting;

2) Equal or proportional rows, except for one, are deleting;

3) Row in a form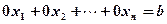, where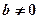, shows that the system has no solution.

Using the last table we rewrite a system in traditional form. If the system has been reduced to a diagonal form, we obtain a unique solution. If the number of equations less then number of unknowns, the system has free unknowns and an infinite set of solutions. In this case we will leave basic unknowns (whose coefficients were key elements) on the left-hand side of equations and other unknowns (free unknowns) we will transfer to the right-hand side of equations.

It gives us a general solution of the system. By assigning any values to the free unknowns, we will get particular solution. Among particular solution we select basic solution in which free unknowns are assigned to zeros.

##	ENGLISH	RUSSIAN
1.	augmented	расширенный
2.	compatible (incompatible)	совместная (несовместная)
3.	infinite	бесконечный
4.	general	общий
5.	particular	частный
6.	basic	базисный
7.	discard	отбросить

Дата добавления: 2014-01-15