Закон Био-Савара-Лапласа

Закон Б-С-Л позволяет определить вектор индукции магнитного поля, создаваемого токами разной формы.

Опыт показывает, что вектор 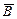пропорционален силе тока, длине проводника, зависит от формы тока и расстояния до рассматриваемой точки. Зависимость 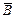от расстояния исследовали для прямого и кругового токов - Био и Савар. Они пришли к выводу, что 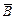в данной точке обратно пропорциональна её расстоянию до тока. Зависимость от формы тока можно учесть, если, по предложению математика Лапласа, ввести понятие элемента тока 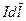. Элементом тока называется вектор, равный по модулю произведению силы тока на элемент длины проводника и направленный вдоль тока.
Рассмотрим ток произвольной формы (см. рисунок). Одна (+) заряженная частица создаёт в точке А магнитное поле с вектором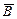, направленным к нам от плоскости чертежа (если точка А лежит в плоскости чертежа).

, где 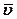- скорость теплового хаотического движения, - дрейфовая скорость упорядоченного движения электрических зарядов под действием электрического поля.

Заряд элемента проводника длины dl, имеющего поперечное сечение S и плотность носителей в единице объема n равен nSdl. Поскольку среднее значение скорости теплового движения электронов <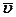>=0, то магнитное поле в точке А, создаваемое элементом длины dl (если взять q=e), так назывемый, элемент вектора магнитной индукции: .

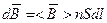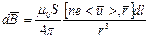, т.к. ne<>=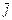, то

, поскольку направления и 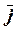совпадают, сделаем замену, 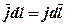,, тогда

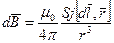, а т.к. Sj=I, то, окончательно, закон Био-Савара-Лапласа в векторном виде может быть представлен следующей формулой:

В скалярном виде индукция магнитного поля, создаваемая элементом тока (закон Био-Савара-Лапласа) принимает вид:

,
где, , r – радиус-вектор, проведенный из элемента тока I dl в точку А. Направление вектора dB перпендикулярно dl и r и по направлению совпадает с касательной к линии магнитной индукции и может быть найдено по правилу правого винта для тока, протекающего через элемент длины dl.

Используя закон БИО-САВАРА-ЛАПЛАСА можно получить формулы:

1.магнитного поля прямого тока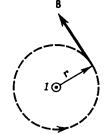

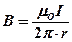
2.магнитного поля соленоида

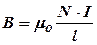
N – число витков катушки соленоида

3.магнитного поля кругового тока

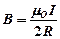
Дата добавления: 2014-01-15