Непрерывность функции

Определение 3.18. Функция 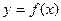называется непрерывной в точке , если выполняются следующие условия: 1) функция определена в точке 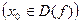; 2) существует конечный предел 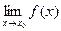; 3) имеет место равенство .

Теорема 3.8. Элементарные функции непрерывны в каждой точке своей области определения.

Замечание. Из условия 2) непрерывности функции 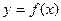в точке следует, что 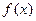определена в двусторонней окрестности .

Следствие 1. Функция 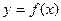является непрерывной в точке , если выполняется предельное соотношение .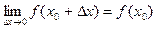

Следствие 2. Функция 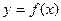является непрерывной в точке , если выполняется предельное соотношение .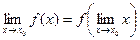

Теорема 3.9. Пусть функци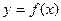и и 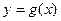непрерывны в точке , тогда непрерывными в данной точке будут сумма 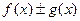, произведение 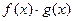и частное (при условии 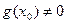) данных функций (справедливость данной теоремы вытекает из определения непрерывности и арифметических свойств предела функции).

С геометрической точки зрения непрерывность функции в точке означает, что график данной функции можно провести через данную точку, не отрывая карандаша от бумаги. Так, например, функция 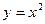является непрерывной в точке 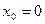, а функция 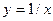- разрывной в точке 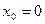(но непрерывной во всех остальных точках числовой прямой).

Определение 3.19. Функция 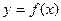называется разрывной в точке , если она определена в двусторонней окрестности , но при этом не выполняется хотя бы одно из условий 1) – 3) непрерывности. Точка называется точкой разрыва функции.

Замечание. Из данного определения и теоремы 3.8 следует, что точки разрыва функции необходимо искать либо среди точек, не входящих в область определения, либо среди точек смены аналитической зависимости.

Определение 3.20. Точка называется точкой устранимого разрыва функции 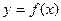, если выполняется условие 2) непрерывности функции, но при этом либо 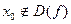, либо .

Пример 3.12. Исследовать на непрерывность функцию .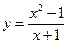

Решение. Поскольку данная функция является элементарной, то единственно возможными точками разрыва являются точки, не входящие в область определения: 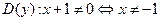. Таким образом, нам необходимо исследовать поведение функции в точке 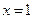: 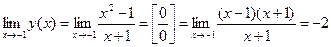. Так как у функции существует конечный предел в данной точке, но в самой точке функция неопределенна, то эта точка является точкой устранимого разрыва.

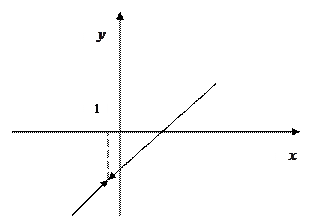
Ответ. Искомая функция является непрерывной во всех точках действительной оси, кроме точки 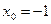. Данная точка является точкой устранимого разрыва.

Определение 3.21. Точка называется точкой разрыва I – го рода функции 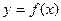, если не выполняется условие 2) непрерывности, а именно: существуют конечные, но не равные между собой односторонние пределы: .

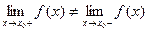Пример 3.13. Исследовать на непрерывность функцию .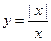

Решение. Перепишем исходную функцию в виде 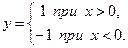Единственно возможной точкой разрыва является точка 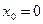, в которой функция не определена. Найдём односторонние пределы: 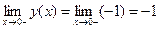, 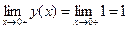. Поскольку они конечные, но не равные между собой, то точка 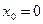является точкой разрыва I – го рода.

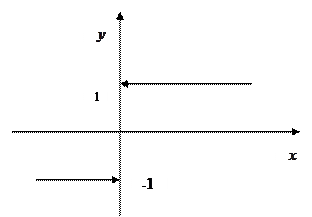
Ответ. Искомая функция является непрерывной во всех точках действительной оси, кроме точки 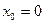. Данная точка является точкой разрыва I – го рода.

Определение 3.22. Точка называется точкой разрыва II – го рода функции 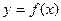, если не выполняется условие 2) непрерывности, а именно: хотя бы один из односторонних пределов равен бесконечности или не существует.

Пример 3.14. Исследовать на непрерывность функцию .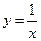

Решение. Поскольку данная функция является элементарной, то единственно возможными точками разрыва являются точки, не входящие в область определения: 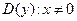. Таким образом, нам необходимо исследовать поведение функции в точке 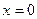: 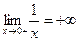– этого достаточно для того, чтобы данная точка была точкой разрыва II – го рода.

Ответ. Искомая функция является непрерывной во всех точках действительной оси, кроме точки 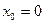. Данная точка является точкой разрыва II – го рода.

Определение 3.23. Точки разрыва I – го и II – го рода называются точками неустранимого разрыва. Таким образом, при классификации точек разрыва определяющим является условие 2) непрерывности.

Пример 3.15. Для функции 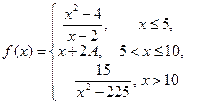необходимо: 1) найти значение параметра 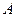из условия непрерывности функции в точке 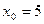; 2) исследовать полученную функцию на непрерывность.

Решение. 1) Воспользуемся определением 3.18 непрерывности: поскольку 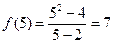, 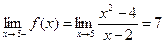и 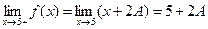, то из равенства 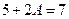находим 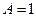. Перепишем исходную функцию в виде

2) Шаг 1. 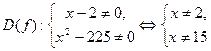– отметим, что мы не стали исключать точку 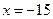, поскольку она не удовлетворяет условию 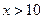. Шаг 2. Точк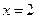и и 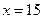являются точно точки разрыва, поскольку в них функция не определена (осталось только их классифицировать); кроме того, необходимо исследовать поведение функции в 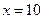– точке смены аналитической зависимости. Шаг 3.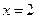: 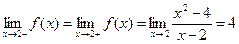поэтому данная точка является точкой устранимого разрыва. Шаг 4. 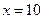: 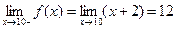, 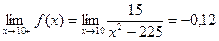поэтому данная точка является точкой разрыва I – го рода (односторонние пределы конечны, но не равны между собой). Шаг 5. 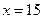: поэтому данная точка является точкой разрыва II – го рода (как минимум один односторонний предел равен бесконечности).

Ответ. Функция является непрерывной на всей числовой оси за исключением точек 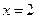(точка устранимого разрыва), 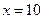(точка разрыва I – го рода), 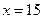(точка разрыва II – го рода).

Определение 3.24. Функция называется непрерывной на интервале 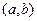, если она непрерывна в каждой точке данного интервала. Функция называется непрерывной на отрезке 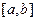, если она непрерывна на интервале 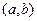, непрерывна справа в точке 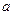и непрерывна слева в точке .

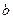Теорема 3.10. Элементарные функции непрерывны на области определения. Без доказательства. Для неэлементарных функций подобное утверждение неверно. Например, функция 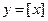определена на всей числовой примой и при этом разрывная при всех целых значениях .

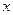Теорема 3.11. (свойства функции, непрерывной на отрезке). Пусть функция 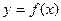непрерывна на отрезке 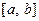, тогда она: 1) ограничена на этом отрезке; 2) достигает на этом отрезке своих наибольшего значения 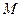и наименьшего значения 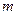; 3) 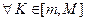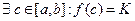- функция принимает все возможные значения из промежутка

Дата добавления: 2014-01-15