Статистические методы обработки экспертной информации

Получаемые от экспертов количественные данные или элемен­тарные суждения в виде ранжировок, баллов, попарных предпочте­ний обрабатываются с целью оценки степени согласованности и компетентности экспертов, а также для получения коллективного (общественного, среднего) мнения экспертной группы. В соот­ветствии с этим при обработке экспертной информации решаются следующие задачи: оценка коллективного мнения экспертной груп­пы; оценка согласованности мнений экспертов; оценка компетент­ности экспертов.

Для решения перечисленных задач разработаны различные ме­тоды, число которых стремительно растет. Рассмотрим наиболее распространенные из этих методов.

Оценка коллективного мнения экспертной группы. Методы оценки коллективного мнения экспертной группы зависят от вида получаемых количественных оценок и элементарных суждений. При оценках в физических единицах оцениваемых величин, балльных оценках, попарных сравнениях используются обычные статистичес­кие методы точечного и интервального оценивания.

Пусть в результате опроса экспертной группы, включающей m членов, получена следующая совокупность чисел:

x _{1 1}, x _{1 2},..., x _{n 1};

x _{1 2}, x _{2 2},..., x _{n 2};

.............

x _{1 m}, x _{2 m},..., x _{n m,}

где x _{i j} - оценка, данная экспертом j объекту i;

n - число оцениваемых объектов.

Предполагается, что каждому объекту соответствует точное значение x_i*, которое может быть получено при m ∞. Тогда средняя коллективная оценка объекта i будет

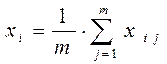
Дисперсия этой оценки

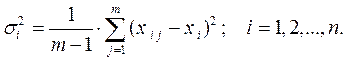
Для определения доверительного интервала I _xi ⁼ (x_i - ε_pi, x_i + ε_pi) с заданной доверительной вероятностью Р можно ис­пользовать точный и приближенный методы. На­иболее практичен приближенный метод, который при большом числе экспертов (m ≥ 10) дает интервальную оценку, близкую к оценке с помощью точного метода. При использовании данного метода ве­личина ε_pi, определяющая границы доверительного интервала, рассчитывается по формуле

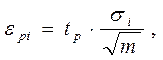
где t _p - коэффициент, зависящий от заданной доверительной вероятности, определяется с помощью таблицы, фрагмент которой для отдельных значений Р приведен в табл. 1.

Таблица 1

Значения коэффициента t_p

Р	0,8	0,85	0,9	0,95
t p	1,282	1,439	1,643	1,960

Таким образом, если имеем значения m = 10; x _i = 5; σ _i² = 4 и задана доверительная вероятность Р = 0,9, то t _p = 1,643 и величина

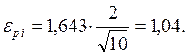
В результате доверительный интервал I _xi ⁼ (x_i - ε_pi, x_i + ε_pi) = (3,96; 6,04),

т.е. значение оцениваемой величины x _i* будет лежать в этом интервале с вероятностью 0,9, или 3,96 < x _i* < 6,04 при Р = 0,9.

При группировке (сортировке) и ранжировании объектов кол­лективная оценка может быть получена в соответствии с простым правилом: объекты i следует располагать согласно суммам S i их рангов (номеров, классов) x _{i j} полученных в результате индивидуальных оценок каждым j -м экспертом. Таким образом, на первое место ставится объект i, сумма рангов которого S _i = x _{i 1} +

x _{i 2} +... + x _{i m} бу­дет минимальной; на второе место - объект l, сумма рангов ко­торого S_l = x _{l 1} + x _{l 2} +... + x _{l m}, занимает следующее по значе­нию место и т.д.

Оценка согласованности мнений экспертов производится с целью выявления подгрупп экспертов с близкими мнениями. При высокой согласованности всей группы коллективная оценка будет единственной. При низкой степени согласованности из общей группы следует выделить подгруппы экспертов, имеющих высокую согласованность, и провести сравнительный содержательный ана­лиз их оценок с целью выявления причин различия точек зрения этих подгрупп. В том случае, если причина заключается в недос­таточной добросовестности экспертов, то следует исключить оценку подгруппы и повторить экспертный опрос.

Методы определения согласованности также зависят от вида оценок.

При оценках в физических единицах величин, балльных оцен­ках, попарных сравнениях согласованность мнений экспертов оце­нивается с помощью коэффициента вариации γ _i, который рассчиты­вается по формуле

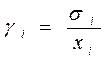
и определяет относительную величину разброса оценок экспертов по отношению к среднему значению коллективной оценки x _i.

При полной согласованности экспертов, когда все x _{i j} = x _i, γ _i = 0. Полагают, что согласованность экспертов удовлетворите­льная, если все γ _i < 0,3, и хорошая, если все γ _i < 0,2.

При группировке (сортировке) и ранжировании объектов сог­ласованность мнений экспертов определяется с помощью коэффици­ента конкордации (согласованности) W, характеризующего степень согласованности мнений экспертов по всем оцениваемым объектам.

Пусть в результате экспертного опроса произведено ранжи­рование объектов, в ходе которого установлены ранги x _{i j} каждо­го i - го объекта j - м экспертом,

i = 1,2,..., n; j = 1,2,..., m.

Тогда коэффициент конкордации определяется следующим образом. Вычисляются суммы рангов i -х объектов

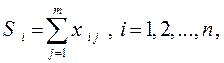
и среднее значение полученных величин

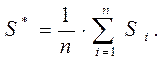
Определяются отклонения d _i сумм S _i от среднего значения S^*: d _i = S _i – S ^*,

i = 1,2,...., n.

Среди множества рангов x _{1 j,} x _{2 j},..., x _{n j}, присвоенных объектам j-м экспертом, определяется количество групп r_j, име­ющих равные ранги, и количество равных рангов t _s в каждой s-й группе.

Допустим, что производится ранжировка n = 9 объектов, ко­торым j-й эксперт присвоил ранги, представленные в табл.2.

Таблица 2

Дата добавления: 2014-01-15