Логические операции и элементы

Шестнадцатеричная система счисления.

Двоично-десятичная система счисления.

Двоичная система счисления.

Десятичная система счисления.

N₁₀ = … + a₂10² + a₁10¹ + a₀10⁰ + …

Весовые коэффициенты a_i имеют десять значений от 0 до 9.Например, десятичное число 531 можно представить следующим образом:

531₁₀ = 5*10² + 3*10¹ + 1*10⁰

N ₂ = … + a₂2² + a₁2¹ + a₀2⁰ + …

Весовые коэффициенты a_i в двоичной системе принимают два значения 0 и 1. Например, двоичный код 1011 можно представить следующим образом:

1011₂ = 1*2³ + 0*2² + 1*2¹ + 1*2⁰

Если просуммировать все разряды, то можно перейти к десятичному эквиваленту двоичного кода, что составляет в данном случае - 11₁₀

Перевод из десятичной в двоичную систему счисления производится разложением десятичного числа по степеням двоичного кода. Например:

37₁₀ = 1*32 + 0*16 + 0*8 + 1*4 + 0*2 + 1*1 = 100101₂

1 0 0 1 0 1 ₂

В данной системе каждый десятичный разряд кодируется отдельными четырьмя двоичными. Например

8 4 2 1 8 4 2 1 8 4 2 1

953 ₁₀ = 1001 0101 0011_{2 - 10}

9 5 3 ₁₀

Отдельные четыре двоичных разряда или десятичный разряд называются декадой. Перевод из двоичной системы в двоично-десятичную и обратно должен сопровождаться промежуточным получением десятичного эквивалента:

1011 1110₂ = 190₁₀ = 0001 1000 0000_{2 – 10}

Десятич.	Шеснад.
…	…
	A
	B
	C
	D
	E
	F

В шестнадцатеричной системе весовые коэффициенты a_i принимают шестнадцать значений от 0 до 15.Значения от 0 до 9 совпадают с десятичными числами, а от 10 до 15 кодируются буквами от А до F. Например, десятичное число 42 в шестнадцатиричной системе имеет вид: 42₁₀= 2*16¹ + 10*16⁰= 2А_16.

При переводе из шестнадцатиричной в двоичную и наоборот, каждый шестнадцатиричный разряд кодируется отдельными четырьмя двоичными.

2А₁₆ = 0010 1010₂ = 42₁₀

Восемь двоичных разрядов или два шестнадцатиричных – образуют байт. Шестнадцатиричная система применяется для более компактного представления двоичных кодов.

В двоичной алгебре (алгебра Буля) производятся различные логические операции над двоичными числами, основными из которых являются:

1. Операция инвертирования (элемент НЕ – инвертор): Х = (читается «Х равно не Х»).

2. Логическое умножение (элемент И): Х·0=0; Х·1=Х; Х·Х=Х; Х·=0;

3. Логическое сложение (элемент ИЛИ): Х+0=Х; Х+1=1; Х+Х=Х; Х+=1;

Как в обычной алгебре, при анализе и преобразовании логических выражений используют распределительный, сочетательный и переместительный законы. Кроме того, широко используются законы инверсии (правила де Моргана):

Логические элементы и их функции представлены таблицей истинности (табл. 4.1.), а условные графические изображения приведены на рис…...

Таблица 4.1.

Вход	Выход
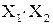
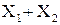
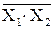
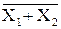
X1	X2	«НЕ»	«И»	«ИЛИ»	«И-НЕ»	«ИЛИ-НЕ»	исключающее«ИЛИ»

Простейшие логические элементы могут объединяться в более сложные ИМС. Так элемент, условное изображение которого представлено на рис., реализует функцию 2´2И´2ИЛИ´НЕ (цифры обозначают количество логических элементов данного вида и количество входов у них).

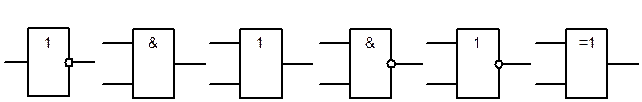
НЕ	И	ИЛИ	И - НЕ	ИЛИ – НЕ	Исключающая ИЛИ
Рис……. Условное обозначение простейших логических элементов

Вместо отдельных инверторов на практике часто применяют многовходовые элементы И-НЕ, включенные по схемам, представленным на рис…...

Простейшие логические элементы могут объединяться в более сложные ИМС. Так элемент, условное изображение которого представлено на рис. 2а, реализует функцию 2´2И´2ИЛИ´НЕ (цифры обозначают количество логических элементов данного вида и количество входов у них).

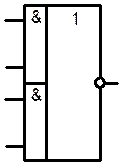
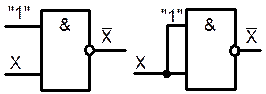
а)	б)
Рис…. Комбинированный логический элемент (а) и схемы включения элементов «И-НЕ» в режиме инвертора (б).

Вместо отдельных инверторов на практике часто применяют многовходовые элементы И-НЕ, включенные по схемам, представленным на рис……..

Дата добавления: 2014-01-15