В области D

Значения подинтегральной функции в области D.

То,где m и M – соответственно наименьшее и наибольшее

7).Если f (х,у) непрерывна в замкнутой области D, площадь которой S, то

в этой области существует такая точка 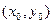), что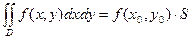

Величину 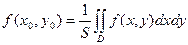называют средним значением функции f (х,у)

1.2.Вычисление двойного интеграла в декартовых координатах.

Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов и осуществляется справа налево.

РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ В

ДВОЙНОМ ИНТЕГРАЛЕ.

Различают два основных вида области интегрирования.

1). Область интегрирования D ограничена слева и справа прямыми

x=x₁ и x=x₂ (x₂>x₁) и снизу и сверху непрерывными кривыми Y= φ₁(x) e Y= φ₂(x)

[ φ₂(x) > φ₁(x)] ,каждая из которых пересекается x=X (x₁<X<x₂) только в

одной точке (рис.2).

Y y= φ ₂(x) 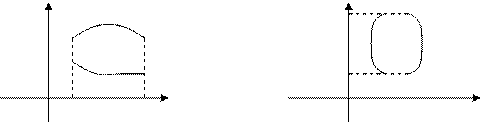y₂ B D · C D x= ψ₂(y)

S x= ψ₁(y ) S · A у=φ₁(x) B y₁ A C

X X

O x₁ x₂ O

Рис.2 Рис.3

Итак,имеем область D={(x,y): x₁<X<x₂, Y₁ <Y< Y₂}, вычисление интеграла может

быть произведено путем сведения к повторному интегралу по формуле

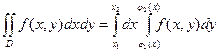, если Y₁= φ₁(x) и Y₂= φ₂(x).

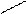2). Область интегрирования снизу и сверху ограничена прямыми y=y₁ e y=y₂ (y₂>y₁),

а слева и справа – непрерывными кривыми x=ψ₁(y) e x= ψ₂(y) [ψ₂(y) > ψ₁(y )],

каждая из которых пересекается с горизонталью y=Y (y₁<Y<y₂) только в одной точке(рис.3). Аналогично предыдущему имеем область: D: D={(x,y): x₁<X<x₂, Y₁ <Y< Y₂}

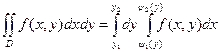_, если x₁= ψ₁(y) и x₂= ψ₂(y).

Если область интегрирования не принадлежит ни к одному из разобранных выше видов,то ее стараются разбить на части,каждая из которых относится к одному из этих двух видов.

ПРИМЕР. Вычислить .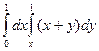

у

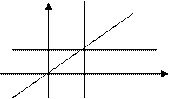^у=х Oбласть D={(x,y):0 ≤x≤1,x≤y≤1}=>x₁=0, x₂=1, y₁=x, y₂=1.

А С Для решения можем использовать как 1,так и 2 вид

у=1 расстановки пределов интегрирования.Область D –

О треугольник.

х=0 х=1

Рис.4.

Уравнениями прямых являются: x=0,y=1,y=x.

1).

.

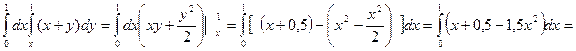
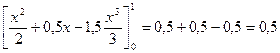2). .

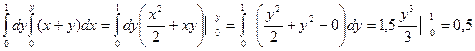ПРИМЕР. Вычислить площадь области,ограниченной кривыми y= 2-x²,y=x.

Область интегрирования ограничена параболой y= 2-x² и прямой y=x.

Найдем точки пересечения этих линий: 2-x²=x или x²+x-2=0 , т.е. x₁= -2 и x₂=1.

.

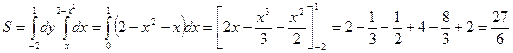ПРИМЕР. Написать уравнение линий,которые ограничивают область интегрирования

и сделать рисунок:

.

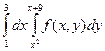Решение:

Нарисуем параболу и прямые:

x₁=1,x₂=3,y₁=x² , y₂=x+9.

Рис.5

1.3.Двойной интеграл в полярных координатах.

Переход из декартовых координат x,y в координаты полярные r,φ производится методом замены переменных:

x = r cos θ, y = r sen θ, где r Є R, 0≤ θ ≤2π, 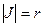следовательно

,

где область D*- область в полярной системе координат,соответствующая

области D в декартовой системе координат.Она ограничена лучами θ=α, θ=β (α < β)

и кривыми r=r₁ (θ), r=r₂ (θ) [r₁ ( θ ) ≤ r₂ (θ) ],т.е. область D*- правильная:луч,выходящий из полюса,пересекает ее границу не более чем в двух точках),то правую часть формулы

можно записать

.

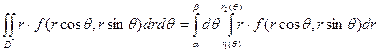Внутренний интеграл берется при постоянном θ, 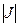-функциональный определитель

Дата добавления: 2014-01-15