
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение оригиналов
|
|
|
|
Если  ,
,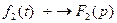 ,то
,то
 ,
,
где путь интегрирования-вертикальная прямая  .
.
σ

γ+i∞
s
s0 γ
γ-i∞
Рис.8
1.3.Резюме.
Рассмотренные свойства преобразования Лапласа представляют собой основные правила операционного исчисления.Для удобства пользования перечислим эти свойства:
1. Линейность. 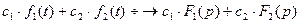 .
.
2. Подобие. 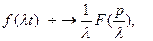
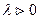 .
.
3. Смещение. 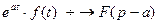 .
.
4. Запаздывание. 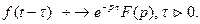
5. Дифференцирование оригинала.
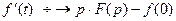 ,
,  ,
,
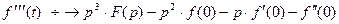 ,
,
…………………………………………………
6. Дифференцирование изображения.
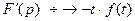
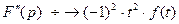
…………………………
7. Интегрирование оригинала. 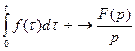 .
.
8. Интегрирование изображения. 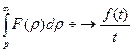 .
.
9. Умножение изображений. 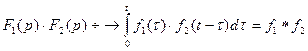 .
.
10. Умножение оригиналов.  .
.
1.4.Таблица оригиналов и изображений.
| № | Оригинал

| Изображение
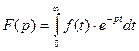
|
| 1. | 
| |
| 2. | 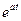
| 
|
| 3. | t | 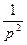
|
| 4. |
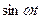
| 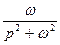
|
| 5. | 
| 
|
| 6. |

| 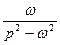
|
| 7. |

| 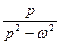
|
| 8. |

| 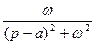
|
| 9. |

| 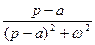
|
| 10. |

| 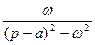
|
| 11. |

| 
|
| 12. |
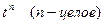
| 
|
| 13. | 
| 
|
| 14. |
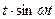
| 
|
| 15. |

| 
|
| 16. |

| 
|
| 17. |
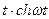
| 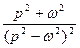
|
| 18. |

| 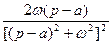
|
| 19. |

| 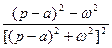
|
| 20. | 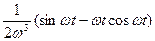
| 
|
| 21. | 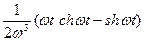
| 
|
| 22. |
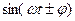
| 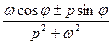
|
| 23. |

| 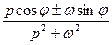
|
§2.Операционный метод решения линейных
дифференциальных уравнений.
Пусть требуется найти частное решение линейного дифференциального
уравнения с постоянными коэффициентами
 , (2.1)
, (2.1)
удовлетворяющее начальным условиям 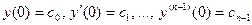 ,
,
где  -заданные числа.
-заданные числа.
Считаем,что искомая функция у(t) вместе с производными и функция f(t)
являются оригиналами.
Пусть  и
и 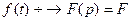 .Пользуясь свойствами
.Пользуясь свойствами
дифференцирования оригинала и линейности,перейдем в уравнении (2.1) от оригиналов к изображениям:
 .
.
Данное уравнение называют операторным (или уравнением в изображениях).
Разрешим его относительно Y:
 ,
,
т.е. 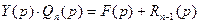 , где
, где  - алгебраические многочлены от
- алгебраические многочлены от
р степени п и п-1 соответственно.
Из последнего уравнения находим  . (2.2)
. (2.2)
Полученное решение называют операторным решением дифференциального уравнения.
Оно имеет более простой вид,если все начальные условия равны нулю,т.е. 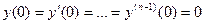 :
:  .
.
Находя оригинал у(t),соответствующий найденному изображению (2.2),получаем
в силу теоремы единственности,частное решение ДУ (2.1).
ПРИМЕР. Решить операционным методом ДУ при условиях
при условиях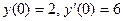 .
.
Пусть  ,тогда
,тогда 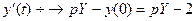 ,
,
 ,
,
 .
.
Подставляя эти выражения в ДУ,получаем операторное уравнение:
 .
.
Тогда 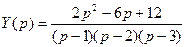 ,найдем у(t). Разобъем дробь на сумму простейших
,найдем у(t). Разобъем дробь на сумму простейших
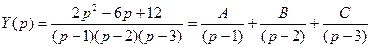 и найдем А,В,С, применив метод неизвестных коэффициентов:
и найдем А,В,С, применив метод неизвестных коэффициентов:

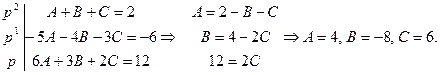
Тогда получаем: 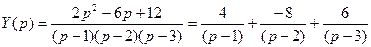 ,
,
 .
.
ПРИМЕР. Найти методом операционного исчисления решение у=f(t) линейного ДУ
 при условиях
при условиях  .
.
Операционное исчисление произведем с помощью преобразований Лапласа.
Если при этом преобразовании функция f(t), 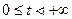 ,переходит в функцию
,переходит в функцию  :
:
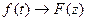 ,
,
то производная  (2.3)
(2.3)
и интеграл  .
.
Следовательно,оператор дифференцирования р переходит в оператор умножения на переменную z, а интегрирование сводится к делению на z.
Решение: перейдя от искомой функции f(t) и данной функции 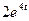 к их изображениям
к их изображениям
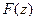 и
и 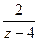 (см.таблицу оригиналов и изображений) и применяя формулу (2.3) для
(см.таблицу оригиналов и изображений) и применяя формулу (2.3) для
изображения производных,получают 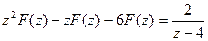 или
или
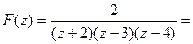
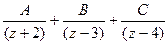 ,
,
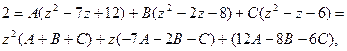
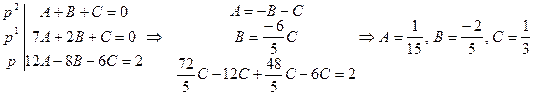 ,
,
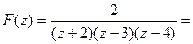
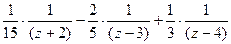 ,
,
Откуда по таблице:  .
.
Домашние задания к теме НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
1.Вычислить интегралы:
а).  ; б).
; б). 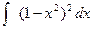 ; в).
; в). 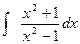 ; г).
; г).  ;
;
д). 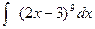 ; е).
; е). 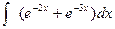 ; ж).
; ж). 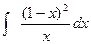 ; з).
; з). 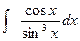 ;
;
и).  ; к).
; к).  ; л).
; л).  ; м).
; м).  ;
;
н). 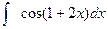 ; о).
; о). 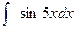 ; п).
; п). 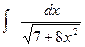 .
.
2.Применяя метод подстановки, найти интегралы:
а).  ; б).
; б). 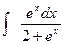 ; в).
; в). 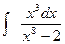 ; г).
; г).  ; д).
; д).  ,(
,( );
);
е).  , (x=-lnt); ж).
, (x=-lnt); ж). 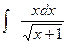 ,(
,(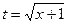 ); з).
); з).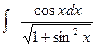 , (t=sinx);
, (t=sinx);
и). 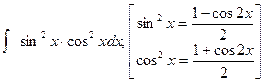 ; к).
; к). 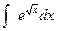 ,(
,( ), л).
), л).  ;
;
м). 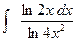 , (t=ln2x).
, (t=ln2x).
3.Вычислить интегралы, применяя формулу интегрирования по частям:
а). 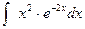 ; б).
; б). 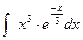 ; в).
; в).  ; г).
; г).  ; д).
; д).  .
.
4. Найти интегралы:
а).  ; б).
; б). 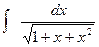 ; в).
; в).  .
.
5. Вычислить интегралы, используя метод неопределенных коэффициентов:
а).  ; б).
; б).  ; в).
; в).  ; г).
; г).  .
.
6.Вычислить интеграл, используя рекуррентную формулу: 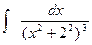 .
.
Домашние задания к теме ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
1.Вычислить определенные интегралы:
а).  ; б).
; б). 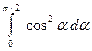 ; в).
; в).  ; г).
; г).  .
.
2.Применяя метод подстановки, найти интегралы:
а).  ; б).
; б). 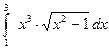 ; в).
; в). 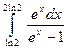 .
.
3.Вычислить интегралы, применяя формулу интегрирования по частям:
а).  ; б).
; б).  ; в).
; в).  .
.
4. Вычислить интегралы, используя метод неопределенных коэффициентов:
а).  ; б).
; б). 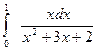 .
.
5.Вычислить несобственные интегралы (или установить их расходимость):
а). 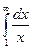 ; б).
; б). 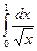 ; в).
; в). 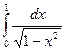 ; г).
; г).  .
.
6.Найти площадь фигуры, ограниченной линиями:
а). ; б).
; б). 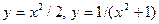 ; в).
; в).  ;
;
г).  ; д).
; д). 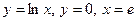 ; е).
; е). 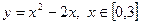 ;
;
ж).  ;
;
з).  .
.
7).Найти длину дуги: 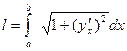
а).  ; б).
; б).  ;
;
в). 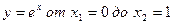 ; г).
; г).  ;
;
д). 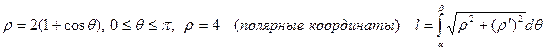 .
.
8.Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями:  вокруг оси Ох. (
вокруг оси Ох. ( ).
).
Домашние задания к теме ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
1.Решить дифференциальное уравнение с разделяющимися переменными:
а).  ; б).
; б).  ;
;
в). 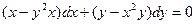 ; г).
; г).  ;
;
д).  ; е).
; е). 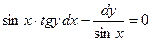 .
.
2. Решить дифференциальное уравнение методом замены переменной:
а). 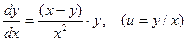 ; б).
; б). 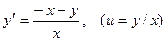 .
.
3. Решить однородное дифференциальное уравнение:
а).  ; б).
; б). 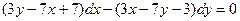 ;
;
в).  .
.
4.Решить задачу Коши:
а).  ; б).
; б). 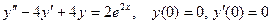 ;
;
в).  .
.
5.Решить линейное дифференциальное уравнение:
а).  ; б).
; б).  ; в).
; в). 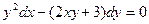 .
.
6.Решить уравнение Бернулли:  .
.
7.Решить дифференциальное уравнение (методом вариации постоянной):
а). 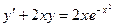 ; б).
; б). 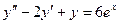 ; в).
; в).  ;
;
г). 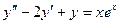 .
.
Домашние задания к теме ЧИСЛОВЫЕ РЯДЫ.
1.Напишите формулу общего элемента ряда:
а). 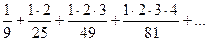 ; б).
; б). 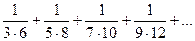 ;
;
в). 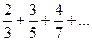 ; г).
; г).  ; д).
; д).  .
.
2.Найдите 5 первых элементов ряда:
а).  ; б).
; б). 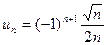 ; в).
; в). 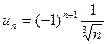 ; г).
; г).  .
.
3.Исследуйте расходимость ряда, используя необходимый признак расходимости:
а).  ; б).
; б).  ; в).
; в).  ; г).
; г).  ; д).
; д).  .
.
3.Используя I критерий сравнения, исследовать сходимость ряда:
а).  ; б).
; б). 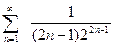 ; в).
; в).  ; г).
; г). 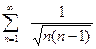 .
.
4. Определить сходимость ряда, используя II критерий сравнения:
а). 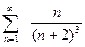 ; б).
; б).  ; в).
; в).  ; г).
; г). 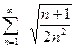 .
.
5. Используя признак Коши, исследовать сходимость ряда:
а).  ; б).
; б).  ; в).
; в). 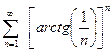 ; г).
; г). 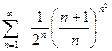 ;
;
д). 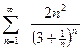 ; е).
; е).  .
.
6.Определить сходимость ряда, используя признак Даламбера:
а). 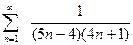 ; б).
; б). 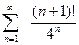 ; в).
; в).  ; г).
; г). 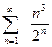 ; д).
; д). 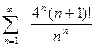 .
.
7. Используя интегральный признак Коши, исследовать сходимость ряда:
а).  ; б).
; б). 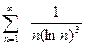 ; в).
; в).  ; г).
; г). 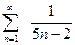 ; д).
; д).  .
.
8.Знакочередующийся ряд. Определить сходимость ряда, используя признак Лейбница:
а).  ; б).
; б).  ; в).
; в). 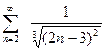 ; г).
; г).  .
.
9.Определить ряд сходится абсолютно, условно или расходится?
а). 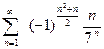 ; б).
; б).  ; в).
; в).  .
.
10.Найти радиус, интервал и область сходимости степенного ряда:
а). 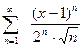 ; б).
; б). 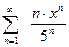 ; в).
; в). 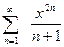 ; г).
; г). 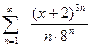 ; д).
; д). 
11.Разложить в степенной ряд по степеням х функцию:
а). 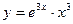 ; б).
; б). 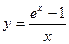 ; в).
; в). 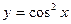 ; г).
; г). 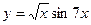 .
.
12.Вычислить приближенно с точностью 0,0001:
а). 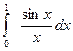 ; б).
; б). 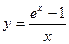 ; в).
; в). 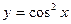 ; г).
; г).  .
.
13.Разложить в ряд Фурье функцию:
а).  ; б).
; б). 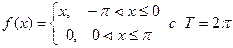 ;
;
14. Разложить по косинусам кратных дуг: 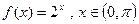 .
.
15.Разложить по косинусам и синусам кратных дуг:
а).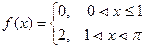 ; б).
; б). 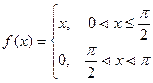 ; в).
; в). 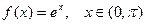 .
.
16. 13.Разложить в ряд Фурье функцию 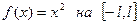 с периодом Т=2.
с периодом Т=2.
17. Разложить по синусам кратных дуг  для вычисления суммы ряда: а).
для вычисления суммы ряда: а).  ; в).
; в). 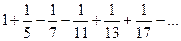 .
.
Домашние задания к теме КРАТНЫЕ ИНТЕГРАЛЫ.
1.Укажите линии и область интегрирования:
а). 
2.Изменить порядок интегрирования:
а). 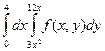 ; б).
; б).  ; в).
; в). 
3.Вычислить:
а).  ; б).
; б). 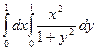 ; в).
; в). 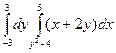
4.Найти объем тела, ограниченного поверхностями:
а).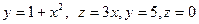 ; б).
; б).  ; в).
; в).  ;
;
г). 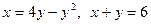 .
.
5. Вычислить массу однородной пластинки, ограниченной линиями 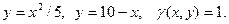
6.Вычислить массу и статические моменты квадратной пластинки со стороной равной 2 и плотностью 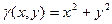 .
.
7.Найти массу и координаты центра тяжести однородной фигуры, ограниченной линиями 
8.Вычислить, используя полярные координаты:
а). 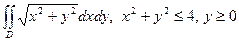 ; б).
; б).  ;
;
в).  .
.
в).объем тела, ограниченного поверхностями
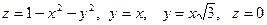 , расположенного в I октанте.
, расположенного в I октанте.
г).момент инерции однородной материальной фигуры относительно оси Ох,
если область D ограничена кардиоидой  .
.
9.Вычислить:
а).  ; б).
; б).  ; в).
; в).  .
.
10.Найти объем тела, ограниченного поверхностями
а). 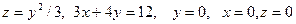 ;
;
б). 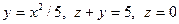 ;
;
в). 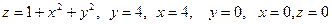 .
.
11.Используя цилиндрические координаты, найти:
объем тела, ограниченного поверхностями
а).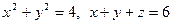 ; б).
; б).  ;
;
в).массу тела, если 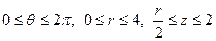 .
.
12. Используя сферические координаты, найти:
а) объем тела, ограниченного поверхностями 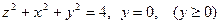 ; б).
; б). 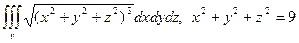 ;
;
в).  .
.
Домашние задания к теме КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ.
1.Вычислить криволинейный интеграл 1-го рода:
а).  , если L- отрезок прямой
, если L- отрезок прямой 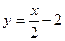 , соединяющий точки А(0,-2), В(4,0).
, соединяющий точки А(0,-2), В(4,0).
б). 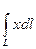 , если L- отрезок прямой
, если L- отрезок прямой 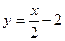 , соединяющий точки А(0,0), В(1,2);
, соединяющий точки А(0,0), В(1,2);
в). 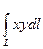 , если L- отрезок прямой, соединяющий точки А(-1,0), В(0,1);
, если L- отрезок прямой, соединяющий точки А(-1,0), В(0,1);
г).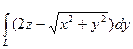 , если L- первый виток конической винтовой линии
, если L- первый виток конической винтовой линии  ;
;
д). 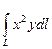 , если L- дуга круга
, если L- дуга круга  , расположенная в первой четверти. (Применить:
, расположенная в первой четверти. (Применить: 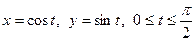 ).
).
2.Вычислить криволинейный интеграл 2-го рода:
а).  , если L- отрезок прямой, соединяющий точки А(2,3),
, если L- отрезок прямой, соединяющий точки А(2,3),
В(3,5);
б). 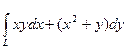 , если L- дуга параболы
, если L- дуга параболы  , соединяющий точки А(0,0),
, соединяющий точки А(0,0),
В(2,4);
в). 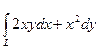 , если L- отрезок прямой, соединяющий точки А(4,2), В(6,3).
, если L- отрезок прямой, соединяющий точки А(4,2), В(6,3).
3.Используя формулу Грина, найти:
а). , взятый вдоль параболы
, взятый вдоль параболы 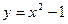 и хорды от точки
и хорды от точки
А(1,0) до В(2,3);
б).  , взятый вдоль ломаной линии ОАВ, если О(0,0), А(1,0),
, взятый вдоль ломаной линии ОАВ, если О(0,0), А(1,0),
В(0,1).
4.Найти массу винтовой линии  , если плотность
, если плотность  .
.
5.Найти массу дуги кривой  , если плотность
, если плотность
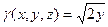 ;
;
6.Вычислить длину однородной дуги линии цепи  .
.
Домашние задания к теме КОМПЛЕКСНЫЕ ЧИСЛА.
1.Доказать, что а). ; б).
; б).  ; в).
; в). 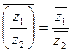 ; г).
; г).  .
.
2.Дано  , найти:
, найти:
а). 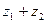 ; б).
; б). 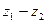 ; в).
; в). 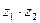 ; г).
; г). 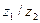 .
.
3.Вычислить: а). ; б).
; б).  ; в).
; в).  .
.
4.Определить действительную и мнимую части комплексных чисел:
а). 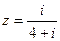 ; б).
; б).  ; в).
; в). 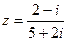 ; г).
; г).  .
.
5.Представить в тригонометрической и показательной форме комплексные числа:
а).  ; б).
; б).  ; в).
; в).  ; г).
; г).  ; д).
; д). 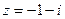 ;
;
е). 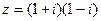 ; ж).
; ж).  ; з).
; з).  .
.
6.Вычислить,используя формулу Муавра:
а). 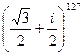 ; б).
; б). 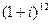 ; в).
; в). 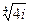 ; г).
; г). 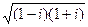 ; д).
; д).  .
.
7.Найти все значения корней и изобразить на комплексной плоскости 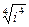 .
.
8.Выполнить действия:
а). 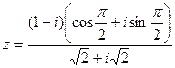 ; б).
; б).  .
.
9.Найти корни уравнения:  .
.
Домашние задания к теме ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ.
1.Найти поверхностный интеграл:
а).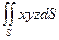 , где S - часть плоскости
, где S - часть плоскости 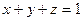 , лежащая в I октанте;
, лежащая в I октанте;
б). 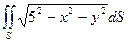 , где S - полусфера
, где S - полусфера 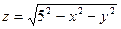 ;
;
в). 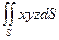 , где S - часть поверхности параболоида
, где S - часть поверхности параболоида 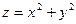 , отсекаемая
, отсекаемая
плоскостью 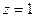 ;
;
г).  , где S - часть конической поверхности
, где S - часть конической поверхности  , расположенная
, расположенная
между плоскостями  .
.
2.Вычислить:
а). 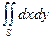 ,где S - внутренняя поверхность конуса
,где S - внутренняя поверхность конуса 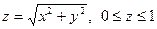 ;
;
б).  ,где S - верхняя часть плоскости
,где S - верхняя часть плоскости  , расположенная
, расположенная
в I октанте;
в).  ,где S - внешняя сторона части сферы
,где S - внешняя сторона части сферы 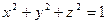 ,
,
расположенной в I октанте.
3.Найти массу поверхности  сферы
сферы 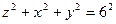 и статический момент
и статический момент
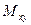 верхней полусферы, если поверхностная плотность
верхней полусферы, если поверхностная плотность 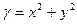 .
.
Домашние задания к теме ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ.
1.Вычислить поток векторного поля 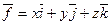 через часть сферы
через часть сферы  , расположенной в первом октанте
, расположенной в первом октанте в направлении внешней нормали.
в направлении внешней нормали.
2.Используя формулу Стокса, найти циркуляцию векторного поля
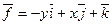 вдоль окружности
вдоль окружности  .
.
3.Найти циркуляцию векторного поля вдоль линии 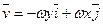 (векторное поле линейных скоростей при вращении твердого тела вокруг оси Оz с угловой скоростью ω).Уравнение окружности задано в параметрической форме:
(векторное поле линейных скоростей при вращении твердого тела вокруг оси Оz с угловой скоростью ω).Уравнение окружности задано в параметрической форме:  .
.
4.Найти дивергенцию и поток, используя формулу Остроградского-Гаусса, если  через полную поверхность конуса
через полную поверхность конуса 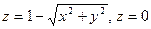 .
.
5.Доказать,что векторное поле  является потенциальным.
является потенциальным.
6.Определить, является ли векторное поле соленоидальным?
а). 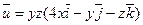 ; б).
; б).  ; в).
; в).  .
.
7.Являются ли данные векторные поля безвихревыми?
а). 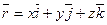 ; б).
; б). 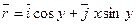 ; в).
; в).  .
.
Домашние задания к теме ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ.
1.Пользуясь определением, найти изображение Лапласа функций:
а).  ; б).
; б).  .
.
2.Может ли функция  быть изображением некоторого оригинала?
быть изображением некоторого оригинала?
3.Найти изображения функций:
а).  ; б).
; б).  ; в).
; в). 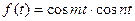 ; г).
; г). 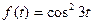 .
.
4.Используя теорему об интегрировании оригинала 
найти изображения: а).  ; б).
; б).  ;
;
в).  ; г).
; г). 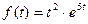 .
.
5.Решить дифференциальное уравнение при заданных начальных условиях операционным методом:
а). 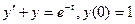 ; б).
; б). 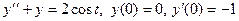 .
.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2866; Нарушение авторских прав?; Мы поможем в написании вашей работы!