Описание дискретных систем в пространстве состояний

Современная теория дискретных систем, так же как и непрерывных, базируется на описании их в пространстве состояний [9].

Рассмотрим дискретную систему m-го порядка с одним входом u[n] и одним выходом y[n], передаточная функция которой в общем виде может быть записана следующим образом

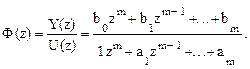(1.122)

Если порядок числителя передаточной функции окажется меньше порядка знаменателя, т.е. l < m, то b₀ =,..., = b _{m-l- 1} = 0.

Из дискретной передаточной функции (1.122) следует разностное уравнение

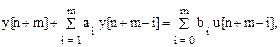(1.123)

которому соответствует структурная схема дискретной системы, приведенная на рис. 1.22.

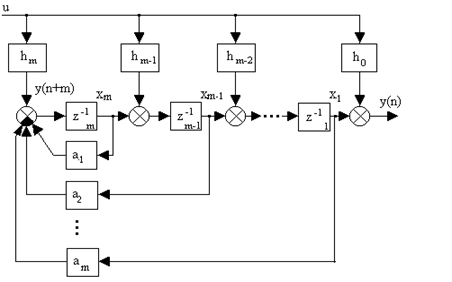
Рис. 1.22. Структурная схема дискретной системы

Обозначив переменные на выходах соответствующих линий задержек через x_i[n] - координаты состояния системы (i= 1, 2,..., m), составим следующую систему из разностных уравнений первого порядка:

(1.124)

Неизвестные коэффициенты h_i (i=0, 1, 2,..., m) определяются из условия эквивалентности системы разностных уравнений (1.124) исходному разностному уравнению (1.123) и вычисляются последовательно по формулам:

h₀ = b₀;

h₁ = b₁ - a₁h₀;

h₂ = b₂ - a₁h₁ - a₂h₀;

..................

В общем виде

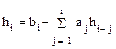, i = 0, 1, 2,..., m. (1.125)

Уравнения (1.124) можно переписать в векторно-матричной форме:

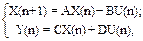(1.126)

где

- вектор переменных состояния;

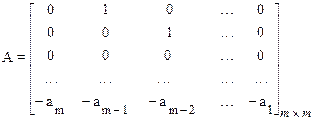- матрица системы;

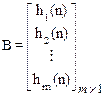- матрица управления;

C = [1 0 0... 0 0 ]_{1 x m} - матрица наблюдения;

D = [h₀]_{1 x 1} - матрица, показывающая влияние входного сигнала на выходную величину системы.

Система уравнений (1.126) является стандартной формой описания дискретной системы в пространстве состояний. Первое уравнение называется векторным разностным уравнением системы, а второе - уравнением выхода.

Стандартной форме соответствует структурная схема системы, изображенная на рис. 1.23.

Рис. 1.23. Структурная схема дискретной системы в матричной форме:

Z^-1 - блок запаздывания; A,B,C,D - блоки матричных усилителей

Переменные состояния - это дискретные значения сигнала в текущий момент времени и m -1 его значений в предыдущие моменты времени.

Аналогично непрерывным системам составляющие вектора переменных состояний x_i[n] рассматривают как оси координат многомерного пространства состояния системы. С течением времени вектор состояния изменяет свое значение и положение, его конец описывает в пространстве состояния некоторую кривую, называемую траекторией движения системы.

Матрица системы A определяет устойчивость и другие показатели качества работы системы, матрица управления B характеризует влияние на переменные состояния входного воздействия, а матрица наблюдения C устанавливает связь выходной величины системы с вектором переменных состояния. Выбор переменных состояния в дискретных системах, как и в непрерывных, является неоднозначной операцией, т.е. векторное разностное уравнение зависит от выбранных переменных состояния. Однако все возможные векторные уравнения эквивалентны, так как описывают один и тот же динамический процесс связи выходной переменной системы с входным воздействием.

В общем случае дискретная система имеет k входов и r выходов. При этом вид векторных уравнений остается таким же (1.126), в которых матрица системы A имеет тот же вид, что и в системах с одним входом и одним выходом, матрица управления становится прямоугольной размером m ´ k, а матрица наблюдения имеет размер r ´ m.

Дискретная матрица переходов устанавливает связь между значениями вектора переменных состояния в различные отсчеты времени и для стационарных систем определяется как [9]

Ф(n) = Z^-1{[zE - A]^-1 z}. (1.127)

Матрицу [zE - A] называют характеристической, определитель этой матрицы образует характеристическое уравнение системы.

Таким образом, решение векторного разностного уравнения имеет вид

(1.128)

Пример. Найти описание в пространстве состояний системы, дискретная передаточная функция разомкнутой цепи которой имеет вид

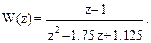
Р е ш е н и е. Определяем дискретную передаточную функцию замкнутой системы

,

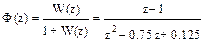которой соответствует разностное уравнение

y[n+2] - 0.75 y[n+1] + 0.125y[n] = u[n+1] - u[n].

На основании выражений (1.125) и (1.126) получаем

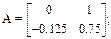
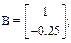С = [1 0]; D = [0].

Уравнения системы в пространстве состояний

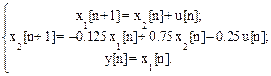
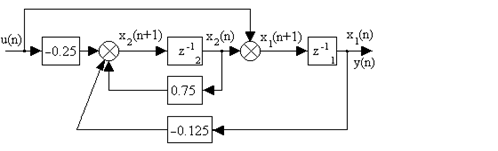
По полученным уравнениям на рис. 1.24,а изображена структурная схема системы, в которой переменные состояния - это выходные величины звеньев задержки.

Найдем полюса (z₁ = 0.5; z₂ = 0.25) дискретной передаточной функции системы и разложим ее на простейшие дроби

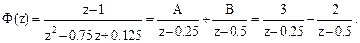
Структурная схема системы представлена на рис. 1.24,б.

а)

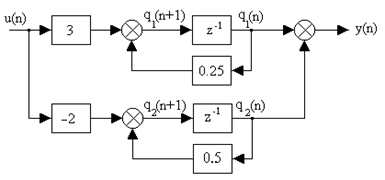
б)

Рис. 1.24. Структурная схема дискретной системы второго порядка:

а - относительно выходов; б - относительно полюсов системы

Выбрав в качестве переменных состояния выходные величины звеньев задержки, получим следующую систему уравнений:

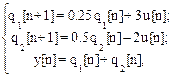
где

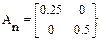
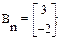С_n = [1 1]; D_n = [0].

В отличие от рассмотренного ранее описания переменные в разностных уравнениях развязаны между собой. Такая запись называется нормальной формой описания дискретной системы в пространстве состояний.

ВОПРОСЫ К РАЗДЕЛУ 1

1. Сформулируйте определение дискретных систем. Какова структура и классификация импульсных систем?

2. Расскажите о математическом аппарате исследования импульсных систем.

3. Сформулируйте теорему Котельникова-Шеннона. Поясните ее физический смысл и практическое значение при проектировании дискретных систем.

4. Поясните методы определения передаточных функций импульсных систем. Каковы особенности передаточных функций статических и астатических систем?

5. Каким образом определяются частотные характеристики импульсных систем?

6. Какими способами определяются переходные процессы в дискретных системах?

7. Сформулируйте условия устойчивости импульсных систем.

8. Каким образом оценивается точность работы импульсных систем?

9. Каков порядок синтеза цифровых систем? Перечислите методы определения передаточных функций корректирующих устройств. Укажите виды структурных схем цифровых фильтров.

10.Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.

содержание глоссарий

Дата добавления: 2014-01-15