Розглянемо, скільки ступенів вільності має кожна вивчена нами сума квадратів

Почнемо з TSS = 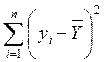. Для створення TSS потрібно (n-1) незалежних чисел, тому що з чисел 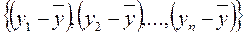незалежні тільки (n-1) завдяки властивості .

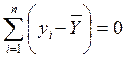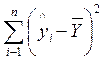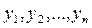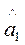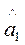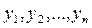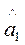
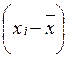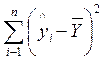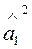
Суму квадратів, що пояснює регресію RSS =, отримують, використовуючи тільки єдину незалежну одиницю інформації, яка утворюється з , а саме . Покажемо, що справді нахил можна передати як функцію від . Запишемо відхилення, що пояснює регресію у вигляді: =. Піднесемо до квадрату: =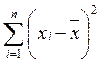. Отже суму квадратів, що пояснює просту лінійну регресію, можна утворити, використовуючи тільки одну одиницю незалежної інформації, а саме 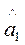. Звідси RSS маєодин ступінь вільності. Ступінь вільності в даному випадку збігається з кількістю незалежних змінних, що входять до регресійної моделі.

Сума квадратів помилок ESS =має (n-2) ступені вільності: кількість спостережень мінус кількість оцінюваних параметрів – два коефіцієнти регресії ,.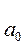

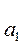У дисперсійному аналізі використовують середні суми квадратів, тобто суми квадратів, поділені на кількість ступенів вільності.

Середнім квадратом помилок називається сума квадратів помилок, поділена на відповідний ступінь вільності, який позначається через MSE:

MSE= / (n-2).

Середнім квадратом, що пояснює регресію, позначають через MSR:

MSR= 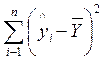/ 1=.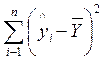

Для загальної суми квадратів середній квадрат не розраховується.

З теорії ймовірності відомо, що величина

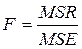
має функцію розподілу F з (1,(n-2)) ступенями вільності.

Перевірка моделі на адекватність за F- критерієм Фішера передбачає здійснення певних етапів:

1. Розраховуємо величину .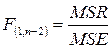

2. Задаємо рівень значимості α.

3. Обчислюємо критичне значення 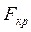за статистичними таблицями F- розподілу Фішера з (1,(n-2)) ступенями вільності.

4. Якщо розраховане нами значення F >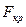, то побудована нами регресійна модель адекватна реальній дійсності.

Дата добавления: 2014-01-11