
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диверсифікація інвестицій і дисперсія доходу
|
|
|
|
Визначимо тепер, що дає диверсифікація для зменшення ризику і виявимо умови, коли ця мета досягається. В якості об’єкту аналізу приймемо деякий абстрактний портфель цінних паперів. Такий вибір пояснюється методологічними перевагами – в цьому випадку простіше виявити залежності між основними змінними. Однак отримані результати можна розповсюдити й на виробничі інвестиції.
У попередньому параграфі ми відмічали, що в якості вимірника ризику в довгострокових фінансових операціях широко розповсюджена така міра, як дисперсія доходу у часі. Диверсифікація портфеля при правильному її застосуванні призводить до зменшення цієї дисперсії при всіх інших рівних умовах. Диверсифікація базується на простій гіпотезі. Якщо кожна компонента портфеля (або вид цінного паперу) характеризується деякою дисперсією доходу, то дохід від портфеля має дисперсію, яка визначається його складом. Таким чином, змінюючи склад портфеля, можна змінювати сумарну дисперсію доходу, а в деяких випадках звести її до мінімуму.
Отже, нехай є портфель з п видів цінних паперів. Дохід від одного паперу виду і складає величину di. Сумарний дохід (А), вочевидь, рівний:
 (6.3)
(6.3)
| 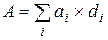 ,
де аі – кількість паперів виду і. ,
де аі – кількість паперів виду і.
|
Для початку положимо, що показники доходів різних видів паперів є статистично незалежними величинами (інакше кажучи, не корелюють між собою). Дисперсія доходу портфеля (D) в цьому випадку знаходиться як:
 (6.4)
(6.4)
| 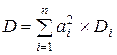 ,
де ,
де 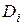 – дисперсія доходу від паперу виду і;
п – кількість видів цінних паперів. – дисперсія доходу від паперу виду і;
п – кількість видів цінних паперів.
|
Для залежних у статистичному змісті показників доходу окремих паперів дисперсію сумарного доходу знаходимо наступним чином:
 (6.5)
(6.5)
| 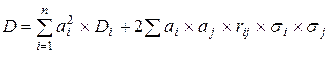 ,
де ,
де 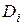 – дисперсія доходу від паперу виду і;
п – кількість видів цінних паперів; – дисперсія доходу від паперу виду і;
п – кількість видів цінних паперів;
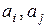 – частки в портфелі паперів видів i та j; – частки в портфелі паперів видів i та j;
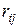 –коефіцієнт кореляції доходу від паперів видів i та j; –коефіцієнт кореляції доходу від паперів видів i та j;
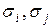 – середнє квадратичне відхилення доходу у паперів видів i та j. – середнє квадратичне відхилення доходу у паперів видів i та j.
|
Коефіцієнт кореляції двох змінних х та у, як відомо визначається за формулою:
 (6.6)
(6.6)
| 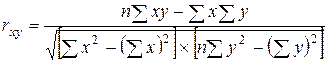
|
і лежить у межах від -1 до +1.
Оскільки коефіцієнт кореляції може бути як позитивною, так і негативною величиною, то, як це випливає з формули (6.5), при позитивній кореляції дисперсія сумарного доходу зростає, при негативній – скорочується. Насправді, при помітній негативній кореляції позитивні відхилення від середнього доходу одних паперів погашаються негативними відхиленнями в інших. І навпаки, при позитивній кореляції відхилення складаються, що збільшує загальну дисперсію та ризик.
Простежимо тепер, який вплив масштабу диверсифікації на розмір ризику. Під масштабом диверсифікації тут будемо розуміти кількість об’єктів, обраних для інвестицій (кількість видів цінних паперів). Звернемося до умовного прикладу, який дозволяє виділити вплив указаного фактору. Отже, нехай портфель складається з паперів різного виду, але таких, що мають однакову дисперсію доходу (σ20). Питома вага в портфелі кожного виду паперів теж однакова, а загальна сума вкладень рівна 1. Нехай показники доходності у окремих видів паперів статистично незалежні, тобто застосовується формула (6.4). Скористуємось наведеною формулою і визначимо дисперсію доходу для портфеля, що складається з двох і трьох видів паперів. Отже, для двох паперів маємо: 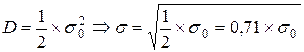 .
.
Для трьох видів паперів квадратичне відхилення портфеля складе 0,58 σ0. Таким чином, зі збільшенням кількості складових портфеля ризик зменшується навіть за однакової дисперсії складових елементів. Однак приріст дієвості диверсифікації зменшується.

| Портфель має складатись із двох видів паперів, параметри яких:
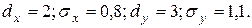 Дохід від портфеля
Дохід від портфеля 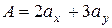 . Таким чином, дохід в залежності від величини часток знаходиться у межах . Таким чином, дохід в залежності від величини часток знаходиться у межах 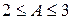 . Дисперсія суми доходу складе: . Дисперсія суми доходу складе:
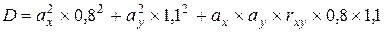 Визначимо дохід і дисперсію для портфеля з частками, рівними, припустимо, 0,3 та 0,7. Одержимо за формулою (6.5):
Визначимо дохід і дисперсію для портфеля з частками, рівними, припустимо, 0,3 та 0,7. Одержимо за формулою (6.5):
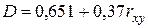 та А = 2,7. Таким чином, при повній позитивній кореляції та А = 2,7. Таким чином, при повній позитивній кореляції 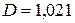 , при повній негативній кореляції , при повній негативній кореляції 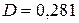 . У підсумку з імовірністю 95% можна стверджувати, що сумарний дохід знаходиться у першому випадку в межах . У підсумку з імовірністю 95% можна стверджувати, що сумарний дохід знаходиться у першому випадку в межах 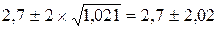 ; другому: ; другому: 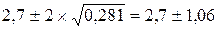 . При нульовій кореляції доходів межі складуть . При нульовій кореляції доходів межі складуть 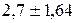 . .
|
Наведені вище вирази для дисперсії сумарного доходу дозволяють розглянути проблему диверсифікації інвестицій і ризику ще в одному аспекті, а саме, – визначити структуру портфеля, яка мінімізує дисперсію, а, отже, ризик. Для знаходження мінімуму дисперсії повернемось до формул, що її визначають. Якщо припустити, що немає статистичної залежності між доходами від окремих видів інвестицій, то знайти оптимальну у вказаному сенсі структуру портфеля не так вже й складно. Припустимо, що портфель, як і раніше, складається з двох видів паперів Х та Y. Їх частки у портфелі складають ах та 1– ах, а дисперсії Dx та Dy. Загальна дисперсія визначається за формулою (6.4). Оскільки ця функція є неперервною, то застосуємо стандартний метод визначення екстремуму. Нагадаємо, що мінімальне значення дисперсії суми має місце, коли:
 (6.7)
(6.7)
| 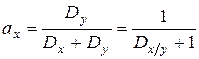 ,
де ,
де 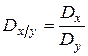 . .
|
За наявності кореляції між показниками доходів звернемось до (6.5). Мінімум цієї функції має місце, коли:
 (6.8)
(6.8)
| 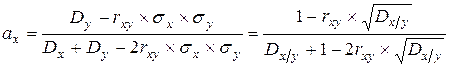 , ,
|
Як видно з наведених формул, розрахункова величина частки одного з паперів може за деяких умов виявитись від’ємною. Звідси випливає, що цей вид паперу просто не повинен включатися в портфель.

| Повернемось до даних попереднього прикладу і визначимо структуру портфеля з мінімальною дисперсією. Нагадаємо, що
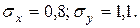 При повній позитивній кореляції розрахункові значення частки першого паперу складуть за формулою (6.8):
При повній позитивній кореляції розрахункові значення частки першого паперу складуть за формулою (6.8):
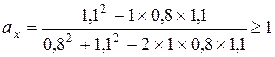 Відповідно
Відповідно 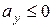 . Отже, мінімальна дисперсія має місце у випадку, коли портфель складається з одного паперу виду Х. Середній дохід від портфеля рівний 2.
При повній негативній кореляції знаходимо: . Отже, мінімальна дисперсія має місце у випадку, коли портфель складається з одного паперу виду Х. Середній дохід від портфеля рівний 2.
При повній негативній кореляції знаходимо:
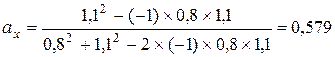
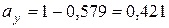 Дисперсія в цьому випадку дорівнює нулю, а середній дохід складе 2,421.
Нарешті, за відсутності кореляції одержимо за формулою (6.7):
Дисперсія в цьому випадку дорівнює нулю, а середній дохід складе 2,421.
Нарешті, за відсутності кореляції одержимо за формулою (6.7):
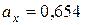 ; ; 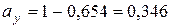 . Дисперсія доходу при такій структурі рівна 0,418, а середній дохід рівний 2,346. . Дисперсія доходу при такій структурі рівна 0,418, а середній дохід рівний 2,346.
|
Перейдемо до загальної постановки задачі і визначимо структуру портфеля з п складовими. Припустимо, що доходи статистично незалежні. Опустимо докази і наведемо результат у матричному вигляді:
 (6.9)
(6.9)
| 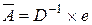 ,
де е – одиничний вектор, що характеризує структуру портфеля, ,
де е – одиничний вектор, що характеризує структуру портфеля,
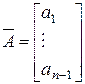 , , 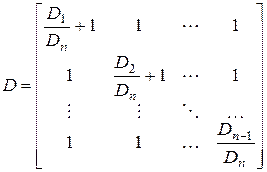 , ,
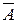 – вектор, що характеризує п –1 елементів структури портфеля.
Матриця D має розмірність – вектор, що характеризує п –1 елементів структури портфеля.
Матриця D має розмірність 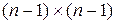 . .
|
Наприклад:

| Експерти оцінили наступні відношення дисперсій для портфеля, що складається з чотирьох видів паперів:
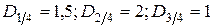 . За формулою (6.9) одержимо: . За формулою (6.9) одержимо:
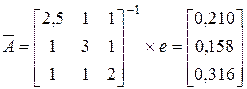 , звідки: , звідки:
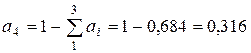 . .
|
Відмітимо, що структуру портфеля, яка мінімізує дисперсію доходу, з п складовими за наявності кореляції визначити так само просто, як це було зроблено вище, неможна. Однак рішення існує, хоча його одержання достатньо клопітка справа.
Аналіз диверсифікації представляє собою перший етап у дослідженні портфеля інвестицій. Наступним є максимізація доходу. Ця проблема також пов’язана з виміром ризику і потребує детального спеціального обговорення, який виходить за межі даного предмету.

| Тому обмежимось лише тезою про те, що метод Г. Марковіца, який заключається у розробці й рішенні спеціальної моделі нелінійного програмування з використання показників доходів і дисперсій, у теоретичному плані не викликає зауважень. |
Що стосується його практичного застосування, то тут, на погляд багатьох спеціалістів, приховані серйозні підводні камені.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 683; Нарушение авторских прав?; Мы поможем в написании вашей работы!