Конденсаторы

Электрические конденсаторы предназначены для создания электрического поля и хранения его энергии.

Электрический конденсатор представляет собой два проводника (обкладки), разделенные слоем диэлект­рика. Промышленностью выпускаются бумажные, элект­ролитические, керамические и другие конденсаторы. В бумажном конденсаторе проводниками являются две длинные ленты алюминиевой фольги, а диэлектриком — ленты парафинированной бумаги. В электролитическом конденсаторе роль диэлектрика выполняет тонкий слой окиси на поверхности обкладки из алюминиевой фольги. Конструкция плоского конденсатора показана на рис. 1.6,а; его условное обозначение — на рис. 1.6,б. Конденсатор обладает свойством накапливать и удержи­вать на своих обкладках равные по величине и разные по знаку электрические заряды. Под зарядом q конден­сатора понимают абсолютное значение заряда одной из обкладок.

Конденсатор можно сравнить с газовым баллоном. Баллон заполняется газом под давлением, а конденса­тор заряжается под действием напряжения (рис. 1.7).

Рис. 1.6 Рис. 1.7

Чем больше напряжение, тем больше заряд конденсатора, поэтому «вместимость» конденсатора оценивается не зарядом, а отношением q/U, которое называется емкостью конденсатора:

C = q/U. (1.6)

Изменение напряжения влечет за собой прямо пропор­циональное изменение заряда конденсатора, поэтому ем­кость конденсатора от напряжения не зависит. Емкость конденсатора численно равна заряду при напряжении один вольт (1).

Единица емкости — фарад (Ф). На практике пользуются более мелкими единицами — микрофарад (1 мкФ = 10^-6 Ф) или пикофарад (1 пФ = 10 ^-12 Ф). Емкость плоского конденсатора определяется по фор­муле

C = εε₀S/d, (1.7)

где S — площадь обкладок; d — расстояние между обкладками. Для создания конденсаторов большой емкости применяют диэлектрики с большой диэлектри­ческой проницаемостью ε.

Следует отметить, что емкостью обладают не только конденсаторы, но и другие элементы электрических устройств, на которых накапливается электрический заряд (провода электрических линий, электроды электронных ламп и др.). Однако нередко емкостью этих устройств принебрегают.

При зарядке конденсатора (рис. 1.7) по проводникам, которыми подключены его обкладки к источнику напря­жения, протекает электрический ток. После зарядки ток отсутствует. Почему? Поступающие в процессе зарядки на обкладки конденсатора заряды отталкивают от себя одноименные вновь прибывающие заряды, т. е. ока­зывают им противодействие. Возрастающее при зарядке напряжение конденсатора Uc направлено встречно току и стремится уравновесить действие напряжения источ­ника U {2).

Зарядка конденсатора продолжается до тех пор, пока Uc < U, и прекращается при

U=U_с

(действие равно противодействию).

Источник напряжения, доставляя заряды на обкладки конденсатора (рис. 1.7), производит работу, значение которой определяется из формулы (1.4): A = Uq. Эта работа численно равна площади графика q(U) (рис. 1.8).

Зависимость заряда q на обкладках конденсатора от напряжения U имеет вид, показанный на рис. 1.9. Площадь графика этой зависимости (по аналогии с рис. 1.8) численно равна энергии электрического поля конденсатора W_э, которая может быть определена как площадь прямоугольного треугольника:

W_э = qU/2. (1.8)

На создание электрического поля конденсатора расходуется только

половина работы источника A = qU. Вторая половина этой работы расходуется на нагрев проводов, по которым заряды проходят на обкладки конденсатора.

Из формулы (1.6) q = CU. Подставив это выражение в (1.8), получаем еще одну формулу для энергии конден­сатора:

W₃ = CU²/2. (1.9)

Во многих случаях для получения нужной емкости конденсаторы приходится соединять в группу, которая называется батареей. Различают параллельное и по­следовательное соединение конденсаторов.

При параллельном подключении С_1, С₂, С₃ к источнику напряжения (рис. 1.10) все конденсаторы зарядятся до одинакового напряжения, равного напряжению источника U = U₁ = U₂ = U₃ (так как каждый конденсатор присо­единен к полюсам источника). При этом энергия бата­реи W_э.б , в соответствии с законом сохранения энергии,

W_э.б=W_э1+W_э2+W_э3(1.10)

Используя формулы (1.9) и (1.10), получаем (учитывая равенство напряжений)

С_б = С₁ + С₂ + С₃

Емкость батареи параллельно соединенных конденса­торов равна сумме емкостей отдельных конденсаторов (3). Рассмотрим последовательное соединение конденсато­ров (рис. 1.11).

На обкладки 1 и 4 заряды поступают от источника питания. Заряды на внутренних обкладках 2 и 3 появляются за счет электростатической индукции. В резуль­тате зарядятся все обкладки конденсаторов.

Разряжаясь,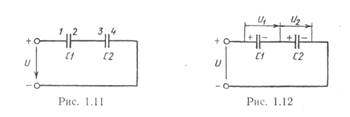батарея отдает заряды с внешних обкла­док. Заряды внутренних обкладок нейтрализуют друг друга, поэтому

q_б = q₁ = q₂

При последовательном соединении конденсаторов за­ряд батареи и каждого конденсатора в отдельности один и тот же (4).

Из формулы (1.6) U — q/C, т. е. при последователь­ном соединении конденсаторов, напряжения на них рас­пределяются обратно пропорционально емкостям от­дельных конденсаторов.

Используя уравнения (1.10) и (1.8) и учитывая равен­ство зарядов, получаем

U=U₁+U₂

(действие равно сумме противодействий)

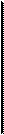Напряжение батареи последовательно соединенных конденсаторов равно сумме напряжений отдельных конденсаторов (5). Поэтому на практике последовательное соединение конденсаторов применяется в тех случаях, когда напряжение источника превышает рабочее напря­жение конденсаторов.

Из положения (5) следует, что q/C_б = q/C₁ + q/C₂, т. е.

l/C_б =l/С₁ + l/C₂. (1.11)

По этой формуле рассчитывается емкость батареи последовательно соединенных конденсаторов. При после­довательном соединении п одинаковых конденсаторов емкость батареи на основании формулы (1.11)

С_б = С/п.

ТЕМА 2. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Дата добавления: 2014-01-15