Варіанти реалізації цінних паперів,тис. Грн

Варіант реалізації ЦП	Стан ринку
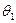
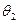
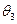
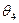
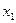
x2

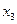
Розв'язування:

Для пошуку оптимального рішення використаємо різні критерії та порівняємо результати.

Критерій Вальда (критерій песимізму). Цей критерій діє за принципом максиміну, тобто забезпечує максимальний прибуток (виручку) з мінімально можливих.

Оптимальним буде таке рішення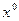, для якого значення виру­чки набуває максимального з мінімально можливих варіантів:

f⁰ =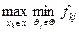

Спочатку кожному варіанту 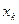присвоюємо, як показник, його гаран­тований рівень доходів:

для першого варіанта х₁: 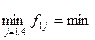{3;6;7;11} = 3;

для другого варіанта х₂: 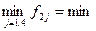{5;10;6;5} = 5;

для третього варіанта х₃: 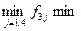{6;8;8;4} = 4.

З цих показників обираємо максимальний: .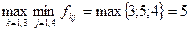

Це значення доходу відповідає рішенню х₂, отже, за критерієм Вальда це рішення буде оптимальним.

Якщо платіжна матриця характеризує втрати, то обирається варіант рішення, який забезпечує мінімальні з максимально мож­ливих втрат (принцип мінімаксу). Обирається таке рішення 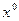,для якого значення платіжної матриці набуває мінімальних з ма­ксимально можливих втрат:

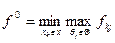
Критерій Вальда розглядає зовнішнє середовище як вороже, аг­ресивно налаштоване до суб'єкта ризику, тому він орієнтується на найгірший стан зовнішнього середовища. Така стратегія є виправданою, наприклад, у тому разі, коли суб'єкт ризику (в даному разі банк) зацікавлений в тому, щоб за­страхуватися від несподіваних програшів.

Величина доходу, що відповідає максимінній стратегії, називається нижньою ціною гри.

Критерій домінуючого результату (критерій оптимізму) визначає варіант, який максимізує максимально можливі виграші для кожного з станів ринку (принцип максимаксу). Оптимальним буде таке рішення x⁰, для якого значення виручки набуває максимального з максимально можливих варіантів: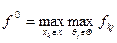

Спочатку кожному варіанту х_k присвоюємо, як показник, його най­більший рівень дохідності:

для першого варіанта х₁: 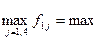{3;6;7;11} = 11;

для другого варіанта х₂: 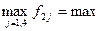{5;10;6;5} = 10;

для третього варіанта x₃: 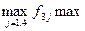{6;8;8;4} = 8.

З цих показників обираємо максимальний:

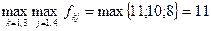
Таке значення доходу відповідає рішенню х₁, отже, за критерієм домінуючого результату це рішення буде оптимальним.

Якщо платіжна матриця характеризує втрати, то обирається варіант рішення, який забезпечує мінімальні з мінімально мож­ливих втрат (принцип мініміну). Обирається таке рішення х⁰, для якого значення платіжної матриці набуває мінімальних з мініма­льно можливих втрат:

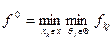
Критерій домінуючого результату звичайно використовується як допоміжний при побудові складніших моделей (наприклад, ієрархічні моделі прийняття багатоцільових або

багатокритеріальних рішень) або ін­ших критеріїв (наприклад, критерій Гурвіца).

Критерій Севіджа (мінімального ризику) дозволяє обрати варі­ант, який за несприятливих умов забезпечує мінімальний ризик. Початковим моментом для цього критерію є перехід від платіжної матриці до матриці ризику R. Елементи даної матриці показують очікувані програші (недоотримані прибутки, виручку) суб'єкта ри­зику при реалізації ним певного рішення залежно від стану ринку.

Розглянемо стан ринку 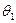. Максимально можлива виручка на цьому ринку 6 тис. грн досягається при реалізації рішення х₃. Якщо суб'єкт ризику реалізує рішення 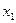, то його невикористані можливості стано­витимуть 6-3 = 3. Для рішення х₂ величина невикористаних можли­востей — 6-5 = 1.

Аналогічно розраховуємо інші елементи матриці невикористаних можливостей. Вибираємо максимальне значення доходу у стовпчику, і від цієї величини віднімаємо величину доходу, що відповідає кожному рішеню (розрахунки наведено в табл. 3.3.4)

Таблиця 3.3.4.

Варіант реалізації ЦП	Стан ринку
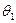
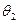
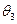
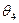
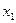
	6-3 = 3	10-6 = 4	8-7=1	11-11=0
хг	6-5 = 1	10-10 = 0	8-6 = 2	11-5 = 6
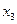
	6-6 = 0	10-8 = 2	8-8 = 0	11-4 = 7
max

Елемент 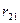= 1 показує, що при стані ринку 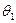та реалізації рішення х₂ банк недоотримає 1 тис. грн.

Оптимальним буде таке рішення 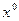, для якого значення невикори­станих можливостей набуває мінімального з максимально можливих варіантів: r⁰ =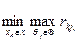

Обчислюємо r_k, k =: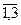

для першого варіанта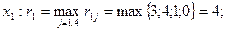

для другого варіанта х₂: r₂= 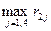= max{l;0;2;6} = 6;

для третього варіанта х_ъ: r_ъ = 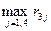= max{0;2;0;7} = 7.

З цих показників обираємо мінімальний:

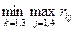= min{4;6;7} = 4.Це значення відповідає рішенню 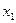, отже, за критерієм Севіджа таке рішення буде оптимальним.

Величина критерію Севіджа для оптимального варіанта нази­вається верхньою ціною гри та відповідає мінімальному програ­шу суб'єкта ризику, котрий обрав один з варіантів, за якого стан ринку найгірший, тобто рішення, обране за цим критерієм, забезпечує гарантова­ний результат.

Критерій Гурвіца — поєднання двох критеріїв: Севіджа та Вальда. За Гурвіцем кожному варіанту рішення відповідає лінійна комбінація тільки найгіршого та найкращого значення доходу. Особливістю цього критерію є те, що середовище є ворожим лише частково.

Ступінь ворожості середовища задається через показник 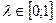При λ=0 критерій Гурвіца збігається з критерієм домі­нуючого результату, середовище сприяє діям суб'єкта прийняття рішення. При λ=1 критерій Гурвіца збігається з критерієм Валь­да, а середовище діє найгіршим чином.

Алгоритм прийняття рішення виглядає так. Спочатку для кожного рішення будується функція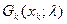, яка залежить від величини λ:

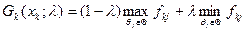
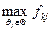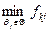де та - відповідно максимальне та мінімальне значення доходу для

варіанта х_к; λ — показник ворожості середовища, λ.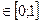

На наступному етапі, якщо відома величина λ, то серед вели­чин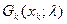

обирається максимальна. Якщо λ не відома, то бу­дується діаграма, за якою визначаються найкращі рішення зале­жно від ворожості середовища.

Обчислимо, 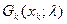, k =:

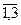для першого варіанта 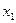: 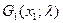= (1-λ)·11+λ·3=11=8·λ;

для другого варіанта х₂: 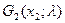=(1-λ)·10+λ·5=10-5·λ;

для третього варіанта х₃: 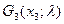=(1-λ)·8+λ·4=8-4·λ.

Оскільки λ нам не відома, то будуємо діаграму (рис. 3.3.1):

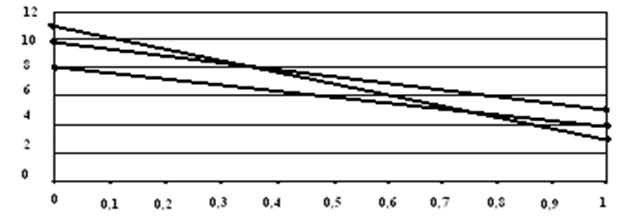
Рис.3.3.1 Лінія Гурвіца

З рис. 3.3.1 видно, що пряма G₃ розміщена нижче прямої G₂. Це означає, що незалежно від ступеня ризиковості середовища рі­шення х₃ забезпечуватиме меншу виручку, ніж рішення х₂. До точки перетину та G₁ та G₂ (нехай у цій точці λ = λ₀) оптимальним буде рішення x₁, тому що пряма G₁, лежить вище прямої G₂, а отже, забезпечується більша виручка від реалізації акцій. На проміжку λ 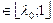найкращим буде рішення х₂.

Визначити величину λ₀ можна, прирівнявши прямі, що перетинаються (G₁, та G₂):

G₁=G₂, 11-8·λ₀ = 10-5·λ₀ => λ₀=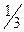

Отже, якщо 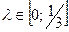, то обираємо рішення 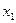, коли ж 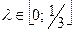, обираємо х₂.

Якщо платіжна матриця характеризує втрати, то функції 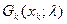будуються так:

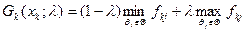
На наступному етапі обирається таке рішення 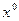, для якого функція 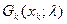набуває мінімального значення.

Висновок: Загалом кількісні методи, як показує практика, дають змогу підвищувати ефективність управління ризиками в банківській справі лише до певної межі, а далі виникають невиправдані ілюзії і ризик зростає. У процесі управління банківськими ризиками ви­никають багатофакторні залежності з численними зворотними зв'язками, які не піддаються формалізації. Коли цим знехтувати, то сутність процесу може настільки спотворитися, що буде дис­кредитовано саму ідею застосування формалізованого математич­ного підходу.

3.4.VaR-методологія кількісної оцінки ризику

Динаміка значень більшості фінансових показ­ників утворює часовий ряд — випадкову величину, яка характери­зується певним середнім (очікуваним) значенням і деяким коли­ванням значень показника навколо цього середнього. Ступінь коливання конкретних значень навколо серед­нього значення ряду кількісно вимірюється показником серед­нього квадратичного відхилення.

Однак, цей показник не є абсолютно адекватним виміром кількості ри­зику. Тому VaR-методологія була розроблена з метою удоскона­лення показників оцінки ризиковості.

На сьогодні VaR-методологія (VaR-метод) є широко визнаним підходом до визначення кількості ризику, зокрема використову­ється для розрахунку потенційних збитків. Застосування VaR.-методології для фінансових та економічних розрахунків грунту­ється на припущенні про те, що значення показника, котрий аналі­зується, є випадковою величиною, яка характеризується нормаль­ним законом розподілу. Графік функції щільності класичного но­рмального розподілу ймовірностей з нульовим середнім значен­ням та одиничним середнім квадратичним відхиленням наведено на рис.3.4.1

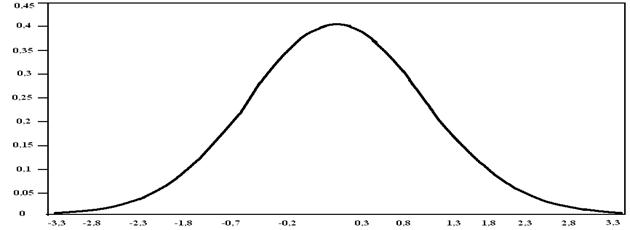
Рис. 3.4.1 Графік функції щільності нормального розподілу ймовірностей з нульовим середнім значенням та одиничним середнім квадратичним відхиленням

Розрахований на основі VaR-методології новий показник вартості, яка перебуває під ризиком є узагаль­нюючим кількісним статистичним виміром ризику. Його називають показником VaR. Цей показник характеризується двома важ­ливими ознаками:

• VaR є виміром ризику, який в одному числі узагальнює вплив різних факторів ризику на інтегральну кількість ризику фі­нансового показника, ризиковість якого вимірюється;

• VaR ураховує кореляцію між впливом різних факторів ри­зику.

Показник VaR характеризується такими трьома параметрами:

• очікуваною кількістю ризику, яка може розраховуватися в абсолютному вимірі або у процентному відношенні до значення показника на певну дату;

• часовим горизонтом, який характеризується очікуваною кіль­кістю ризику (на практиці залежно від специфіки використання значення VaR такими горизонтами найчастіше можуть бути день, тиждень, декада, місяць або рік);

• імовірністю (рівнем довіри), з якою максимальні збитки не перевищать розрахованої очікуваної кількості ризику — ризико­вої вартості (як правило, обирають імовірність 95 або 99 %).

Отже, застосування VaR-методу дає змогу відповісти на запи­тання: якими можуть бути максимальні збитки на вибраному ча­совому горизонті з певною ймовірністю?

Для використання VaR-методу необхідною є наявність випад­кової величини з упорядкованою множиною (рядом) значень 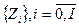, де (I + 1) — кількість значень, доступних для прове­дення розрахунків. Одним з обов'язкових початкових етапів роз­рахунків за VaR-методом є розрахунок на базі ряду значень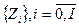змін початкових значень , які звичайно розраховуються за однією з таких формул:

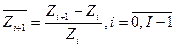(3.4.1)

або

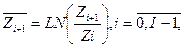(3.4.2)

які на практиці є однаково ефективними

Причиною застосування формул (3.4.1) або (3.4.2) є необхідність певного «нормування» ряду значень переведенням мінливості абсолютних величин значень ряду до форми, в якій у випадку 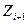< Z_i величина 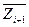відповідної зміни значень набуватиме від'ємних значень, тоді як у випадку 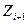> Z_i — додатних.

Зазвичай ризиковими вважаються зменшення значень показника, що аналізується, відносно попере­днього значення.

На практиці найчастіше застосовують три варіанти VaR-методу: історичний VaR-метод, метод Монте-Карло та парамет­ричний (варіаційно-коваріаційний) VaR-метод.

Дата добавления: 2014-01-11