Метод Монте-Карло. Метод Монте-Карло розрахунку VaR є кількісним методом, який моделює майбутні значення змінної за допомогою імітації її поведінки в майбутньому

Метод Монте-Карло розрахунку VaR є кількісним методом, який моделює майбутні значення змінної за допомогою імітації її поведінки в майбутньому. Цей підхід передбачає застосування генератора випадкових значень, вхідними параметрами якого є розподіл імовірностей, середнє значення часового ряду, що моде­люється, і його середньоквадратичне відхилення. З виходу гене­ратора після кожного його запуску знімаються значення конкрет­ного часового ряду. Зауважимо, що після кожного запуску генератора значення отриманих числових рядів будуть дещо ін­шими, хоча всі вони характеризуються заданим середнім значен­ням та значенням середньоквадратичного відхилення.

Важливість застосування методу Монте-Карло для розрахунку VaR полягає в тому, що на початку аналізу у ризик-менеджера є лише один історичний статистичний часовий ряд значень відпо­відної випадкової величини, що для отримання адекватних висновків про поведінку значень цієї величини у майбутньому мо­же бути недостатнім. Метод Монте-Карло дозволяє розширити базу статистичних даних за допомогою моделювання.

Параметричний (варіаційно-коваріаційний) VaR-метод

Параметричний метод передбачає, що значення часового ряду випадкової величини, що аналізується, апріорі має нормальний розподіл. Таким чином, для подальшого аналізу не­обхідно розрахувати лише дві величини — очікуване (середнє) значення та середньоквадратичне відхилення σ, які повністю характеризують класичний нормальний розподіл. Ці значення розраховуються за формулами:

, (3.4.3)

де — очікуване (середнє) значення;

— похідний ряд значень змін початкових значень , розрахованих за формулами (3.4.1) або (3.4.2); N — кількість значень цього ряду;

(3.4.4)

де σ - середньоквадратичне відхилення.

Знаменник формули (3.4.4) дорівнює N, а не (N-1), оскільки у даному викладі вважаємо ряд значень генеральною, а не вибірковою сукупністю, що важливо для невеликих значень N.

Перевагою параметричного методу є стандартна нормальна форма кривої щільності ймовірності, за якої апріорі відомо, що для обчислення волатильності випадкової величини, яка харак­теризується таким розподілом, з імовірністю 95 % необхідно по­множити стандартне квадратичне відхилення на коефіцієнт 1,65, тоді як з імовірністю 99 % — на коефіцієнт 2,33:

ω(95%) = 1,65 • σ; ω(99%) = 2,33 • σ.

Розраховані за даними прикладу 3.4.1 середнє значення, середньоквадратичне відхилення та значення волатильності будуть такими:

= 0,01; σ = 0,14; ω(95%) = 0,23; ω(99%) = 0,32.

Побудований за такими даними графік нормального розподілу має вигляд (рис. 3.4.2)

Рис. 3.4.2 Графік нормального розподілу ймовірностей

Як бачимо, значення волатильності, обчислене з імовірністю 95% за історичним методом (0,15) і параметричними методом (0,23) дещо різняться через те, що ряд значень, розрахованих для прикладу 3.4.1 за формулою (3.4.2), неадекватно представляє нормальний розподіл.

3.5. Оцінювання складових факторів ризику валютного портфеля банку

Найефективніше потенціал і переваги паралельного методу можна продемонструвати на прикладі оцінки можливої майбутньої зміни вартості портфеля валютних коштів.

Алгоритм розрахунку ризикової вартості

Можливі обсяги майбутньої зміни загальної вартості портфеля валютних коштів Р_t розрахованої у базовій валюті (валюті розрахунку), обчислюється за формулою:.

(3.5.1)

де Р_t — часовий ряд значень вартостей усього портфеля валют­них коштів у базовій валюті на дату

t (t =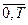, де T+ 1 — кіль­кість значень часового ряду Р_t);

— вартість у базовій валюті компонента портфеля в i-й валюті;

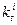— обмінний курс і-ї валюти портфеля до базової валюти на дату t (i = 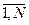, де

N — кількість валют у портфелі);

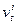— обсяги і-ї валюти у портфелі на дату і (в одиницях валют).

Розглянемо етапи алгоритму розрахунку ризикової вартості VaR, яка відображає можливі обсяги майбутньої зміни вартості портфеля валютних коштів Р_t.

Етап 1. Розрахунок щоденної зміни валютних курсів.

Значення щоденної зміни курсів валют портфеля розраховується за формулою:

(3.5.2)

де 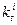— значення обмінного курсу і-ої валюти до базової валюти на дату t, ;

— значення обмінного курсу і-ої валюти до базової валю­ти на дату t -1.

Логарифм темпу зміни валютного курсу характеризує інтен­сивність зміни валютного курсу і є випадковою величиною, роз­поділ якої близький до нормального з середнім значенням, близь­ким до нульового.

Етап 2. Розрахунок волатильності валют.

Для розрахунку волатильностей кожної валюти окремо, без урахування її зв'язку з іншими валютами портфеля, необхідно обчислити для кожної валюти середнє значення та стандартне квадратичне відхилення часового ряду її змін 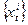(за формулами, аналогічними (3.4.3) та (3.4.4)):

(3.5.3)

де 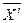— очікуване (середнє) значення часового ряду змін ,

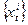(3.5.4)

де 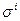- середньоквадратичне відхилення часового ряду змін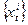

Потім для безпосереднього розрахунку волатильності валют скористаємося формулою: (3.5.5)

де 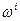— волатильність і-ї валюти; к — постійний коефіцієнт, який для обчислення волатильності валют з імовірністю 95 % дорівнює 1,65, з імовірністю 99 % — 2,33.

Необхідність віднімання середнього значення від волатиль­ності і-ї валюти обумовлюється тим, що, по-перше, на практиці середнє значення, розраховане за формулою (3.5.3), не дорівнює нулю і, по-друге, ризикованим для оцінювання обсягів можливо­го зменшення вартості портфеля вважається лише зменшення обмінних курсів валют до базової валюти (тобто ревальвація ба­зової валюти протягом двох послідовних днів). Значення ж серед­нього квадратичного відхилення розраховується відносно серед­

нього значення , тому за нормального закону розподілу пози­тивність середнього значення означає, що серед значень ряду 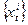переважають позитивні, тобто протягом двох послідовних днів спостерігалося більше позитивних змін, ніж негативних. У цьому разі ступінь ризику для загальної вартості портфеля є меншою.

Для випадку негативного середнього значення міркування прямо протилежні.

Етап 3. Визначення ризикової вартості компонента портфеля в і-й валюті.

Величина ризикової вартості VaR окремого компонента портфеля в і-й валюті обчислюється за формулою:

(3.5.6)

Оскільки волатильність і-ї валюти за формулою (3.5.5) визна­чена на одноденному інтервалі, то й ризикова вартість VaR інтер­претується як максимально очікуваний обсяг зниження загальної вартості окремо взятого компонента валютного портфеля в і-й валюті протягом одного дня з імовірністю 95 % або 99 % залежно відзначення коефіцієнта к у формулі (3.5.5).

Етап 4. Розрахунок кореляційної матриці валют порт­феля.

Взаємні зміни обмінних курсів валют портфеля можуть мати статистичний взаємозв'язок. Наприклад, якщо протягом двох послідовних днів зростає обмінний курс однієї валюти, то здебільшого також спостерігається збільшення або зменшення обмін­них курсів деякої іншої валюти портфеля. Це означає, що зазна­чені валюти мають так звану позитивну або, відповідно, негатив­ну кореляцію. Випадок, коли валюти портфеля мають негатив­ну або незначну позитивну кореляцію, є корисним для змен­шення ймовірного зниження загальної вартості портфеля, оскі­льки у цьому разі зниження вартості однієї валюти може компенсуватися підвищенням вартості іншої. У ризик-менеджменті такий ефект називається структурним хеджуванням ризикової вартості портфеля валютних активів, що за інших рів­них умов дає змогу менеджерам валютних портфелів підібрати валютну структуру з максимально можливим структурним хе­джуванням.

Для врахування взаємної корельованості обмінних курсів валют портфеля при обчисленні його ризикової вартості необ­хідно розрахувати кореляційну матрицю валют портфеля, для чого спочатку потрібно розрахувати коваріації Сij можливих комбінацій рядів випадкових величин 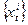і за формулою:

(3.5.7)

Після цього коефіцієнти кореляції Kij випадкових величин розраховуються за формулою:

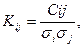(3.5.8)

Квадратна матриця розмірністю n*n, в якій на перехресті і-го рядка j-го стовпчика розташований елемент, що дорівнює Кij, є кореляційною матрицею обмінних курсів валют портфеля. Ця матриця симетрична: Кij =Kji для всіх i,j =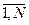, елементи її голов­ної діагоналі Сii дорівнюють 1.

Етап 5. Розрахунок сукупної оцінки можливих втрат VaR загальної вартості валютного портфеля.

Сукупна оцінка можливих втрат загальної вартості валютного портфеля Var розраховується на основі ризикових вартостей VaR окремих валют портфеля і кореляційної матриці обмінних курсів валют за формулою (3.5.9):

VaR= (3.5.9)

де - вектор-рядок окремих ризикових вартостей складових

портфеля в і-й валюті;

- кореляційна матриця обмінних курсів валют портфеля до базової валюти;

— транспонований вектор-рядок окремих ризикових вартостей компонент портфеля в і-й валюті.

Ризикова вартість VaR інтерпретується як максимальний очікуваний обсяг зниження компонента валютного портфеля в і-й валюті протягом одного дня з імовірністю (рівнем довіри) 95% або 99% залежно від значення коефіцієнта k у формулі (3.5.5)

Для оцінювання ефективності структурного хеджування портфеля валютних активів розраховують відповідний коефіцієнт за формулою:

(3.5.10)

де 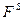- коефіцієнт структурного хеджування (у процентах);

значення VaR для портфеля в цілому без урахування кореляцій між обмінними курсами валют портфеля.

Приклад 3.5.1

Розрахунок ризикової вартості портфеля з чотирьох валют представлений у табл.3.5.1

Таблиця3.5.1

Дата добавления: 2014-01-11