Лекция № 19

Дифференциальное уравнение установившейся фильтрации упругой жидкости и газа по закону Дарси

До сих пор мы рассматривали фильтрацию несжимаемого флюида r=const (без учета уравнения состояния флюидов, т.к. характеристики k, m и m считали постоянными). Эти допущения приводили к простому дифференциальному уравнению фильтрации

DР = 0 и DФ = 0.

Если флюид сжимаем, нужно получить новое дифференциальное уравнение для упругого (сжимаемого) флюида из уравнения неразрывности потока:

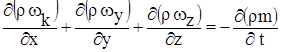
и уравнения движения:

, .

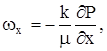
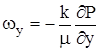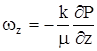Введем функцию Â так, что ее дифференциал

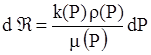или .

Функция Â называется функцией Л.С. Лейбензона. Т.к. Â = Â(х, у, z, t) и Р = Р(х, у, z, t) дифференциал можно переписать

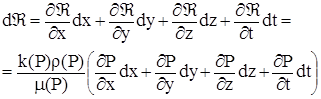, где:

.

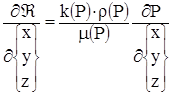Переходя от объемных скоростей (w) к массовым скоростям (rw)

,

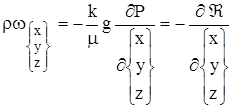и подставляя их в уравнение неразрывности, получим дифференциальное уравнение фильтрации упругого флюида в однородной пористой среде по закону Дарси

.

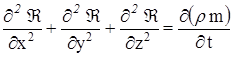В случае установившейся фильтрации

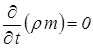и DÂ = 0.

Таким образом, для установившейся фильтрации движения упругого флюида в однородной среде по закону Дарси справедливо уравнение Лапласа, но уже не относительно давления (Р) или потенциала (Ф), а относительно функции Лейбензона Â.

Введение функции Лейбензона в уравнения позволяет установить полную аналогию между установившейся фильтрацией несжимаемого флюида, для которого законы фильтрации нами были уже рассмотрены, и фильтрацией сжимаемого флюида.

В дальнейшем изложении будем считать, что m и k постоянны. Тогда выражение функции Лейбензона упростится:

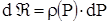и .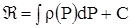

Аналогия заключается в том, что все формулы, полученные для установившейся фильтрации несжимаемого флюида по закону Дарси можно использовать и для установившейся фильтрации сжимаемого флюида в пластах той же геометрии и при тех же граничных условиях, заменив переменные:

Упругий флюид Функция Лейбензона 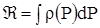Массовый расход флюида массовая скорость фильтрации

Несжимаемый флюид

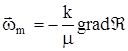
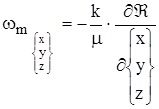
Давление Р

Обменный расход флюида

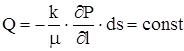
объемная скорость фильтрации

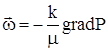
4.2. Установившаяся фильтрация упругой жидкости.

Найдем выражение функции Лейбензона для упругой, но слабо сжимаемой жидкости, описываемой уравнениями состояния

.

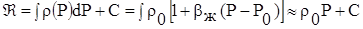Для случая, когда b_ж (Р - Р₀) мало Â 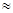r₀Р + С и уравнение фильтрации приводится к виду: .

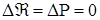Т.е. при установившейся фильтрации упругой (слабосжимаемой) жидкости она в большинстве случаев ведет себя как несжимаемая и можно воспользоваться всеми ранее выведенными формулами. В этом случае метод аналогии параметров применять не надо. Однако, при фильтрации жидкости в пласте с очень высоким пластовым давлением и при большой депрессии надо учитывать ее упругие свойства и рассчитывать функцию Лейбензона и применять метод аналогии.

Рассмотрим применение метода аналогии на конкретных примерах фильтрации упругого газа.

4.3. Установившаяся фильтрация газового потока.

В отличие от жидкости газ значительно более сжимаем и на практике функцию Лейбензона и метод аналогий параметров в основном применяют к газовым потокам.

Рассмотрим методику применения на простых моделях фильтрации.

4.1.1 Прямолинейно-параллельный фильтрационный поток

идеального газа

Предварительно найдем функцию Лейбензона для идеального газа, используя уравнение состояния

,

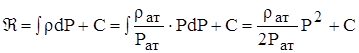где: 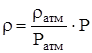- функция состояния r = r (Р).

Для нахождения фильтрационных характеристик газового потока используем метод аналогий параметров между потоком несжимаемой жидкости и течением сжимаемого газа.

Находим распределение давления в потоке идеального газа:

.

Подставляя в последнюю формулу значение функции Лейбензона получим:

.

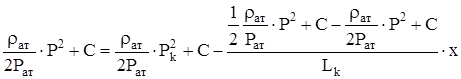Отсюда находим изменение давления в пласте:

.

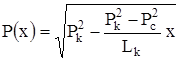Находим градиент давления по такой же схеме:

,

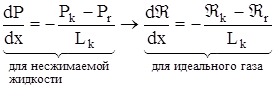подставляем сюда функци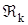и и 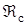, а также производную функции

,

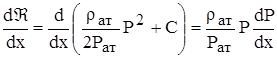получим:

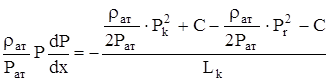, откуда

.

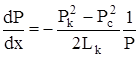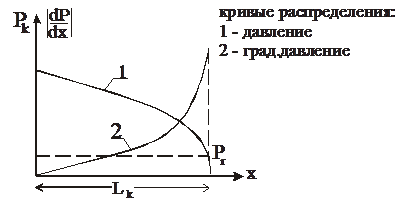Как видно, в отличие от несжимаемого флюида изменение давления в плоскопараллельном потоке подчиняется нелинейной зависимости, а gradP не остается постоянным и возрастает при приближении к галерее. Распределение давления и его градиента в потоке показаны на рис. 19.1.

	Рис. 19.1

Объемный расход газа находим из формулы массового дебита, где вместо Р фигурирует функция Лейбензона Â:

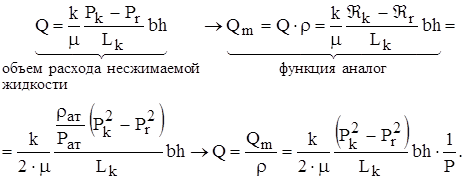
Таким образом, дебит газа зависит от давления (а значит от координаты x).

Скорость фильтрации газа получим. разделив объемный дебит на площадь сечения пласта:

.

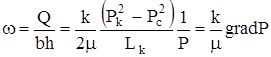Т.о., скорость фильтрации пропорциональна grad P и график ее поведения аналогичен градиенту. Физически возрастание скорости в фильтрационном потоке объясняется расширением газа при снижении давления.

Средневзвешенное давление газа в пласте определим прямым расчетом:

; ; ,

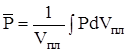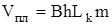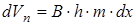интегрируем:

.

4.1.2. Плоскорадиальный фильтрационный поток идеального газа по закону Дарси.

Напомним, что плоскорадиальный поток имеет место в круговом пласте радиусом R_k, в центре которого имеется совершенная скважина радиусом r_c. Характеристики потока в такой модели найдем по методу аналогий, зная характеристики подобного потока несжимаемой жидкости и выражение функции Лейбензона.

Распределение пластового давления газа.

.

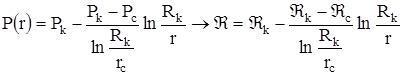Подставляя значения функции Лейбензона , получим

,

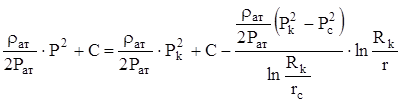откуда .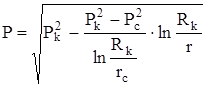

На рисунке 19.2 видно, что в газовом потоке по сравнению с жид-костным, воронка депрессии охватывает меньшую область возмущения, но характеризуется более высокими градиентами давления вблизи скважины.

Градиент давления в пласте

;

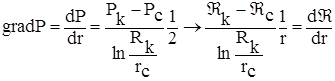; и ;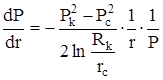

т.о., градиент давления вблизи скважины резко возрастает как за счет уменьшения координаты r, также и падения давления Р.

Дебит газовой скважины получим из формулы Дюпюи, подставляя вместо объемного дебита (Q) массовый (Q_m,), а вместо давления (P) функцию Лейбензона (Â):

или

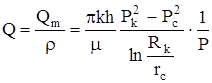,где: .

Нужно иметь в виду, что ввиду неразрывности массового потока

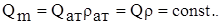Дебит измеряют на устье скважины при атмосферном давлении поэтому: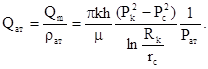

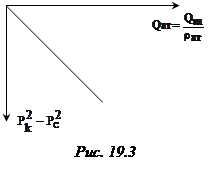Индикаторная диаграмма при фильтрации газа в координатах 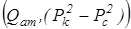- имеет вид прямой линии (рис. 19.3). Скорость фильтрации получим, разделив дебит на площадь сечения фильтрации (S = 2prh)

,

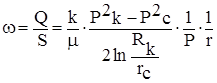Комментарий к скорости фильтрации тот же, что и к градиенту давления. Средневзвешенное по объему порового пространства пластовое давление

,

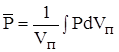где: ; ;

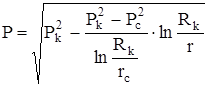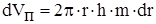, подставляя и интегрируя, получим

Расчеты показывают, что значение 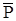при различных (Р_k, Р_c, R_k и r_c) близко к контурному 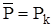. Физически это объясняется локальным характером и значительной крутизной воронки депрессии при притоке газа к скважине. Средневзвешенное 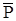используется при определении запасов газа в пласте, а также для приближенного расчета гидродинамических характеристик; замена его контурным давлением значительно упрощает расчеты.

4.1.3. Плоскорадиальный фильтрационный поток идеального газа по двухчленному закону фильтрации.

Лекция № 20.

Вблизи высокодебитных газовых скважин происходит нарушение закона Дарси поэтому расчеты, связанные с разработкой газовых месторождений, а также исследованием скважин, проводят обычно по двучленному закону фильтрации. При этом нельзя использовать дифференциальное уравнение фильтрации (DФ = 0 или DÂ = 0 для установившегося движения), т.к. они выведены в предположении справедливости закона Дарси.

Будем интегрировать непосредственно 2-х членное уравнение закона фильтрации, которое для плоскорадиального потока имеет вид:

,

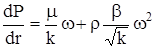где: 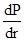- градиент давления, m - вязкость, k – проницаемость, r - плотность в радиальном потоке, b - коэффициент, w - скорость фильтрации.

Найдем распределение давления в круговом пласте и выведем формулу притока газа к скважине. Для этого выразим скорость фильтрации через приведенный объемный дебит используя формулу .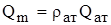

,

где: Q_aт – объемный дебит, приведенный к атмосферному давлению на устье скважины и пластовой температуре; Р – пластовое давление; Q_m – массовый дeбит.

Подставляя выражение w в уравнение фильтрации, получим:

.

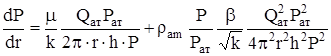Разделяем переменные

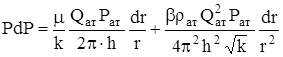
и интегрируем от давления на забое (р = р_с, r = r_с) до давления в произвольной точке пласта (р,r):

.

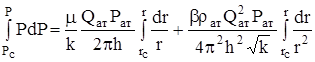Откуда

.

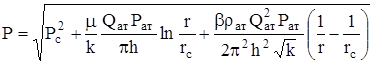Интегрируя снова дифференциальное уравнение от давления на забое, но теперь до давления на контуре питания (Р = Р_к, r = R_к) и пренебрегая 1/R_к по сравнению с 1/r_с, получим уравнение притока газа к скважине

.

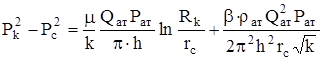Вводя обозначения А и В, приведем его к виду:

,

где: 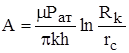и .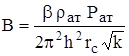

При В = 0 из уравнения притока 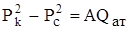получаем:

,

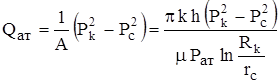что совпадает с ранее полученным уравнением приведенного дебита газа при линейной плоскорадиальной фильтрации.

Коэффициент пропорционален гидропроводности пласта 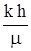, которая в основном определяется его проницаемостью:

~.

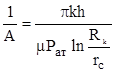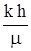Полученное выше уравнение называется уравнением притока газа к скважине.

Коэффициенты фильтрационных сопротивлений А и В определяются опытным путем по данным исследования скважин при установившихся режимах эксплуатации. Газовая скважина исследуется на пяти-шести режимах, задаваемых через изменение забойного давления (давление в скважине Р_с). На каждом режиме измеряют приведенный дебит (Q_ат) и забойное давление (Р_с) (по давлению на устье). Затем скважину закрывают и давление в остановленной скважине принимают за контурное - р_к. После этого по полученным точкам в координатах (, Q_aт) строят индикаторную кривую. Она представляет собой параболу с выпуклостью к оси дебитов. Для нахождения коэффициентов А и В, полученное уравнение нужно линеализировать:

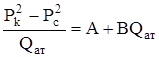
и перестроить в координатах 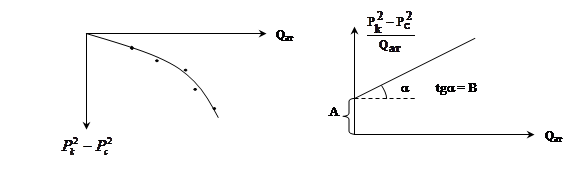(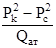, Q_ат) (рис. 20.1).

Рис. 20.1

Уравнение притока газа к скважине широко используется в расчетах при проектировании разработки газовых месторождений. Кроме того, по найденному значению А можно определить коллекторские свойства пласта, например коэффициент гидропроводности:

.

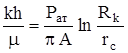4.1.4. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.

Если пластовое давление выше 10 МПа, а депрессия не слишком мала (р_с/р_к £ 0.9), то уравнение состояния газа значительно отличается от идеального газа и плотность газового потока определяется не по закону Клапейрона-Менделеева, а по формуле:

,

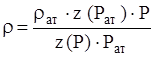где: z(P_aт) и z(P) – коэффициенты сверхсжимаемости при соответствующих давлениях.

Кроме того, для высоких пластовых давлений нужно учитывать зависимость вязкости от давления

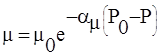или .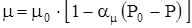

Проницаемость будем считать постоянной.

Функцией Лейбензона в этом случае будет выражение:

Â.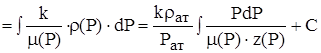

Найдем дебит скважины при плоскорадиальном движении, используя аналогию между установившейся фильтрацией несжимаемой жидкости и газа. Для чего заменим в формуле Дюпюи объемный дебит массовым, а 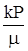- значениями функции Лейбензона:

®

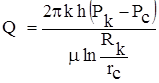где: (приращение функции Лейбензона заменяем определенным интегралом).

Затем получаем объемный дебит газа при атмосферном давлении

.

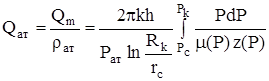Существует несколько способов вычисления интеграла в формуле. Наиболее распространен следующий способ. По графикам зависимости z(Р) и m(Р) определяют значения z(Р_c) = z_с, z(Р_к) = z_к и m(Р_с) = m_с, m(Р_к) = m_к, а переменные под знаком интеграла z и m заменяются их средними значениями из значений на контуре и в скважине:

; .

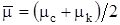Тогда интеграл легко вычисляется и объемный дебит, приведенный к атмосферному давлению принимает вид:

.

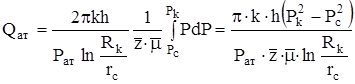Нетрудно видеть, что выражение дебита реального газа отличается от выражения идеального газа множителями 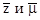в знаменателе.

Второй способ заключается в вычислении определенного интеграла при подстановке в него функций.

, .

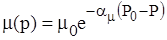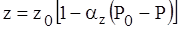4.1.5. Фильтрационный поток реального газа по двухчленному закону фильтрации к несовершенной скважине.

Вначале составим и запишем уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине. Оно будет совпадать с аналогичным уравнением для идеального газа, но со множителями 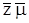в коэффициентах А и В:

.

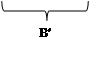
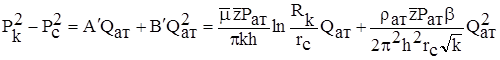Несовершенство газовых скважин при соблюдении закона Дарси учитывается так же, как и несовершенство нефтяных скважин, т.е. радиус скважин в формуле дебита заменяется приведенным радиусом, равным

.

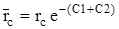Первая зона имеет радиус R₁ = (2-3)r_с. Здесь имеет место нарушение закона Дарси из-за больших скоростей фильтрации вблизи перфорированных отверстий и проявляется несовершенство скважин по характеру вскрытия.

Вторая область представляет кольцевое пространство (R₁<r<R₂), где R₂» h. Здесь также имеет место нарушение закона Дарси, проявляется несовершенство скважины по степени вскрытия и применим двухчленный закон фильтрации.

В третьей зоне R₂<r<R_к – имеет место плоскорадиальный поток, подчиняющийся закону Дарси. Для этой области можно записать:

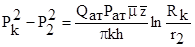- уравнение Дарси для реального газа.

Во второй области примем, что толщина пласта переменна и меняется по линейному закону h (r) = a + b r, где a и b определены из условий h=b при r = R₁, h (r) = h при r = R₂.

Чтобы получить закон движения в этой области надо снова проинтегрировать двухчленный закон фильтрации, подставив в него вместо h выражение h(r). Признав это, получим:

.

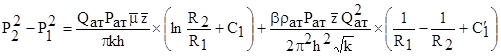Здесь С₁ и С₁¢ - коэффициенты, характеризующие несовершенство скважины по степени вскрытия.

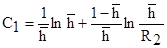; , где .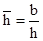

В первой области, где фильтрация происходит по двухчленному закону и имеет место несовершенная скважина по характеру вскрытия, уравнение движения будет аналогичным, но отличатся постоянными С₂ и С₂¢.

.

Коэффициент С₂ определяется по специальным графикам В.И. Щурова:

,

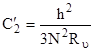где: N – суммарное число перфорированных отверстий, R_u - глубина проникновения пуль в пласт.

Складывая почленно уравнения в трех зонах, окончательно получим:

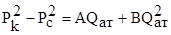, где

, .

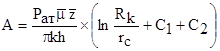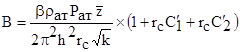Дата добавления: 2014-01-15