Приклад. 40. Задачі, які приводять до визначеного інтеграла (*)

План.

40. Задачі, які приводять до визначеного інтеграла (*).

41. Поняття визначеного інтеграла (*).

42. Властивості визначеного інтеграла (**).

43. Формула Ньютона – Лейбніца (**).

44. Способи обчислення визначених інтегралів (***).

45. Невласні інтеграли (*).

17.1 Задачі, які приводять до визначеного інтеграла.

Означення. Криволінійною трапецією називається плоска фігура, що обмежена лініями: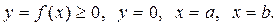

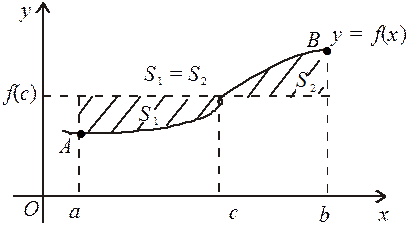
На малюнку зображені: класична криволінійна трапеція та її окремі випадки.

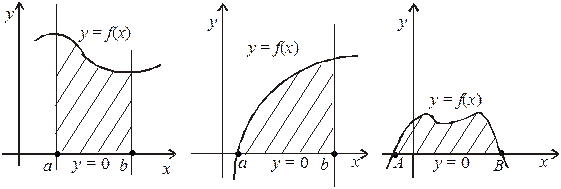
Задача. Обчислити площу криволінійної трапеції аАВв.

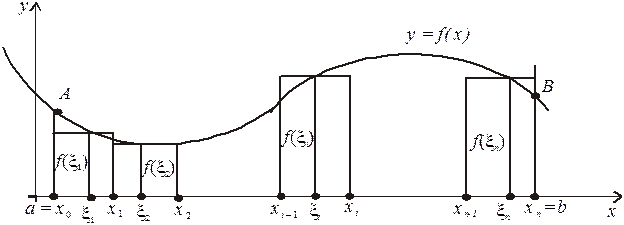
Розіб’ємо проміжок [ a; b ] на n частин точками 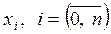так що 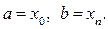Виберемо точки 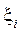так: Побудуємо прямокутники з основою і висотою .

Площа елементарного прямокутника 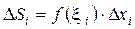. Площа ступінчастої фігури буде тим менше відрізнятись від площі криволінійної трапеції S_aABb, чим менша довжина , а в граничному випадку ці площі будуть збігатися, тобто

Задача. Обчислити роботу змінної сили 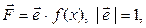що виконується при переміщенні матеріальної точки на проміжку .

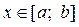Розіб’ємо проміжок [ a; b ] на n частин точками На кожному з відрізків вважатимемо, що сила стала і дорівнює , .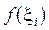

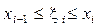Елементарна робота сили на відрізку буде 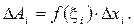Робота А сили 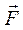на відрізку [ a; b ] знайдеться тоді так:

Означення. Сума вигляду 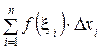називається інтегральною сумою.

Оперувати поняттям інтегральної суми доводиться у процесі розв’язку різних задач. Взагалі інтегральна сума може залежати від способу розбиття проміжка [ a; b ] на частини 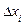, а також від вибору на них точок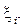

17.2 Поняття визначеного інтеграла.

Нехай 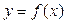— деяка функція, що задана на проміжку [ a; b ]. Розіб’ємо [ a; b ] на n частин точками x_i так що:

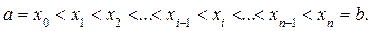
Обчислимо де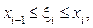

Складемо інтегральну суму: .

Позначимо .

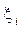Означення. Якщо існує скінченна границя інтегральних сум S_n при і не залежить від способу розбиття [ a; b ] на частини і від вибору точок , то ця границя називається визначеним інтегралом від функції 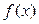на проміжку[ a; b ] і позначається:

,

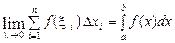де — знак визначеного інтеграла;

а, b — нижня та верхня межі інтегрування;

f (x) — підінтегральна функція;

f (x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

За означенням, визначений інтеграл 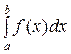— число, яке залежить від типу функції та проміжку [ a; b ]; він не залежить від того, якою буквою позначена змінна інтегрування: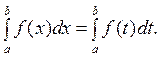

Означення. Функція, для якої на [ a; b ] існує визначений інтеграл 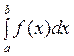називається інтегровною на цьому проміжку.

Геометричний зміст визначеного інтеграла: Якщо , то дорівнює площі відповідної криволінійної трапеції.

17.3 Властивості визначеного інтеграла.

І. Якщ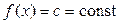о , то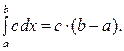

ІІ. Сталий множник можна виносити з-під знака визначеного інтеграла, тобто

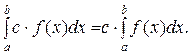
ІІІ. Якщо та 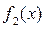інтегровні на [ a; b ], то:

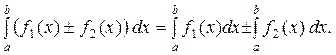
IV. Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто:

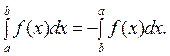
V. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю

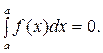
VI. Якщо 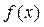— інтегровна в будь-якому із проміжків: [ a; b ], [ a; c ], [ с; b ], то

VII. Якщо і інтегровна для то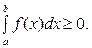

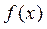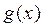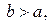VIII. Якщо , — інтегровні та для то

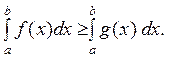
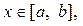
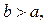IX. Якщо f (x) — інтегровна та для то

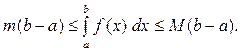
Х. Теорема. Якщо функція 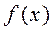— неперервна для то знайдеться така точка що:

Геометричний зміст теореми про середнє полягає в тому, що існує прямокутник із сторонами 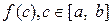та b–a, який рівновеликий криволінійній трапеції аАВв за умови, що функція 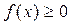та неперервна на проміжку [ a; b ].

17.4 Формула Ньютона—Лейбніца.

Теорема. (Ньютона—Лейбніца). Якщо функція f(x) — неперервна для то визначений інтеграл від функції f(x) на проміжку 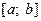дорівнює приросту первісної функції f(x) на цьому проміжку, тобто

де

Позначимо дію подвійної підстановки так: 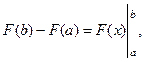тоді зв’язок між визначеним та невизначеним інтегралами можна подати такою рівністю:

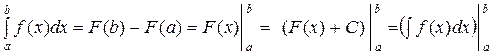
Наслідок. Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.

Приклад.

17.5 Способи обчислення визначених інтегралів.

Теорема (метод підстановки). Якщо:

1) — неперервна для ;

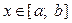2)

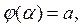
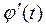3) та — неперервні для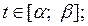

4) при то

Зауваження. При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування, і тому нема потреби повертатись до початкової змінної.

Приклад.

=

Теорема (інтегрування частинами). Якщо функції u(x) та v(x) мають неперервні похідні для , то

17.6 Невласні інтеграли.

Нехай f (x) інтегровна для будь-якого скінченного 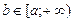, так що існує.

Означення. Границя 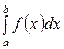при 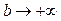називається невласним інтегралом від функції f(x) на нескінченному проміжку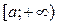і позначається так: .

Якщо ця границя існує та скінченна, то невласний інтеграл називається

збіжним, а якщо не існує (зокрема нескінченна), то – розбіжним.

Якщо f (x) — інтегровна для скінченних a та b, тобто формули для обчислення невласних інтегралів на нескінченному проміжку мають вигляд:

де

Приклад. Дослідити на збіжність інтеграл Діріхле .

Для розв’язування задачі розглянемо такі три випадки:

I. р = 1. 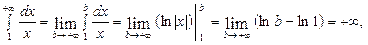інтеграл розбіжний.

II. p < 1. 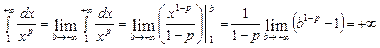, інтеграл розбіжний.

III. p > 1.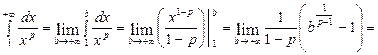

, інтеграл збіжний.

Отже, інтеграл Діріхле збіжний при p > 1 та розбіжний при .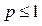

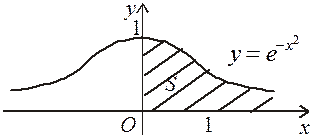Крім безпосереднього обчислення невласних інтегралів при дослідженні їх на збіжність існують і інші методи. Одним із таких методів можна встановити збіжність інтеграла Пуассона.

Особливість інтеграла Пуассона 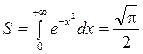полягає в тому, що первісна для підінтегральної функ­ції не виражається через елементарні функції.

У деяких випадках достатньо вста­новити лише збіжність чи розбіжність розглядуваного інтеграла, при цьому можна скористатися методом порівняння, що базується на такій теоремі:

Теорема. Якщо при виконується нерівність , то зі збіжності інтеграла випливає збіжність інтеграла або з розбіжності випливає розбіжність .

Звичайно, для порівняння вибирається інтеграл, збіжність якого відома, наприклад інтеграл Діріхле.

Приклад. Дослідити збіжність інтеграла .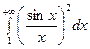

Тоді:.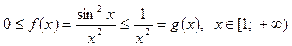

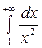— збіжний, як інтеграл Діріхле із р = 2 > 1, тому буде збіжним і .

Розглянемо обчислення невласних інтегралів від розривних (необмежених) функцій. Нехай f(x) неперервна на проміжку та при х = а має розрив 2-го роду.

Означення. називається невласним інтегралом від розривної (необмеженої) функції .

Якщо ця границя існує, то інтеграл називається збіжним, а якщо не існує, то – розбіжним.

Для обчислення таких невласних інтегралів використовують такі формули:

— точка розриву f(x),

.

— точка розриву f(x),

III. — точка розриву f(x),

Зауваження. До невласних інтегралів, які мають точку розриву, що є внутрішньою для не можна застосувати формулу Ньютона—Лейбніца.

Приклад. Обчислити .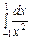

Маємо: , - точка розриву 2-го роду функції — невласний.

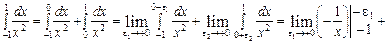
інтеграл розбіжний.

Контрольні запитання.

34. Що називається криволінійною трапецією?

35. Що називається визначеним інтегралом? В чому полягає його геометричний зміст?

36. Які властивості визначеного інтеграла відомі?

37. Запишіть формулу Ньютона-Лейбниця, поясніть її складові.

38. Що називається невласним інтегралом? Поясніть методи їх обчисленння. Наведіть приклади.

Розділ 18. Застосування визначеного інтеграла.

Дата добавления: 2014-01-15