Регрессионный анализ

Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели.

Уравнение линейной регрессии имеет вид:

Y=a₁X₁ + a₂X₂ + …+ a_kX_{k ,} где а₁, а₂… а_{k –} параметры, подлежащие определению методом наименьших квадратов (МНК). В среде MS Excel для этого используется встроенная функция ЛИНЕЙН и инструмент Регрессия из Пакета анализа.

Задание 1. Исследование связей между двумя исследуемыми признаками.

Условие задачи: По 20 туристическим фирмам были установлены затраты на рекламную кампанию и количество туристов, воспользовавшихся после ее проведения услугами каждой фирмы. Определить коэффициент корреляции между исследуемыми признаками.

Ход выполнения:

1. Откройте новую книгу MS Excel и создайте таблицу согласно рис. 1:

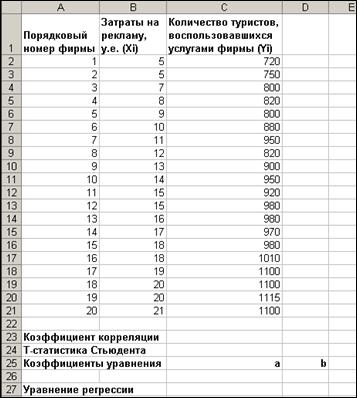
Рис.1.

2. Рассчитайте в ячейке С23 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические. Синтаксис функции:

КОРРЕЛ (массив1; массив 2):

где массив1 – ссылка на диапазон ячеек первой выборки (X);

массив2 – ссылка на диапазон ячеек второй выборки (Y).

В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B21;C2:C21)

3. Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов.

4. Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н₀: r_xy=0 и альтернативная Н₁: r_xy≠0. Для проверки гипотезы Н₀ рассчитайте t-статистику Стьюдента по формуле, указанной выше в ячейке С24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 и формула будет следующей: =C23*КОРЕНЬ(20-2)/КОРЕНЬ(1-(C23*C23))

5. Сравните полученное значение с критическим значением t_ν,α распределения Стьюдента. (При ν =18 и доверительной вероятности α = 0,05, t_{ν,α,табл} = 1,734). Сделайте вывод о наличии связи между исследуемыми величинами.

Задание 2. Построение регрессионной модели.

Дата добавления: 2014-01-15