Специальный алгоритм поиска допустимого решения Т-задачи

(метод минимального элемента)

Ниже будет рассмотрен специальный алгоритм, имеющий эвристический характер, эффективно использующий приведенные выше свойства и совершенно отличающийся от применяемого выше метода минимизации невязок (эвристика – это правило, основанное на опыте человека, его рассуждениях, не имеющих четкого математического обоснования). Забегая вперед, необходимо сказать, что этот алгоритм ориентирован на последующее применение специального алгоритма поиска оптимального решения, реализующего все основные этапы симплекс метода. Поэтому выходом алгоритма является не только само допустимое решение, определяемое матрицей перевозок, но и соответствующий ему базис, а точнее – базисное множество, размерность которого определяется свойством 7, а признак базисности – свойством 8.

В рассматриваемом алгоритме применяется следующая система правил:

1) Заполнение матрицы перевозок 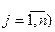производится последовательно, в соответствии с первоначально сформированным, а затем с корректируемым массивом упорядоченных пар (MUP). MUP – это массив, в котором все пары , 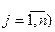выстраиваются в определенную последовательность по возрастанию коэффициентов целевой функции . При этом в первую очередь будут формироваться перевозки, соответствующие меньшим значениям указанных коэффициентов. Отсюда и название рассматриваемого метода: «Метод минимального элемента».

Здесь необходимо сказать, что MUP может быть сформирован и по более простому правилу (по естественному расположению пар индексов в матрице перевозок). Метод, реализующий такое правило, называется «методом северо-западного угла», т.к. матрица начинает заполняться с верхнего левого угла. Это не повлияет на остальную логику алгоритма, но существенно, как показали исследования, влияет на эффективность формируемого базисного решения. Под эффективностью начального допустимого базисного решения здесь понимается его близость к оптимальному решению по числу дальнейших итераций алгоритма поиска оптимального решения.

Как правило (за исключением отдельных частных случаев исходных данных), время, затрачиваемое на формирование MUP по методу минимального элемента, существенно окупается дальнейшей его экономией на этапе поиска оптимального решения.

2) При работе алгоритма используются первоначально определяемые, а затем итеративно изменяемые массивы:

– определяет количество не вывезенной продукции из i -го ПХ (первоначально , );

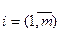; – определяет величину неудовлетворенного спроса на продукцию в j -ом ПП (первоначально , ).

После определения очередной перевозки элементы и корректируются:

(1.155)

3) Очередная определяемая перевозка формируется в соответствии со следующим соотношением:

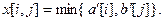(1.156)

Это правило фактически определяет максимально возможную перевозку из i -го пункта производства в j -ый пункт потребления на данный момент работы алгоритма. Соответствующая пара (i, j) заносится в параллельно формируемое начальное базисное множество и удаляется (вычеркивается) из MUP.

. (1.157)

Реализация этого правила обеспечивает то, что число пар (i,j), введенных в множество на первом, основном этапе работы алгоритма формирования допустимого решения, не превысит требуемой размерности базиса (m+n- 1), а в методе минимального элемента дополнительно обеспечивает большую эффективность базисного решения.

4) После использования предыдущих двух правил на очередной итерации алгоритма могут реализоваться следующие случаи: либо , либо 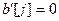, либо и то и другое произойдет вместе. Тогда следующим естественным образом можно доопределить элементы матрицы перевозок:

– если , то все незаполненные к данному моменту элементы в матрице перевозок в i -ой строке обнуляются, и соответствующие пары удаляются из MUP;

– если 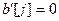, то все незаполненные к данному моменту элементы в матрице перевозок в j -ой строке обнуляются, и соответствующие пары удаляются из MUP;

– если одновременно 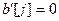, то оба предыдущих пункта выполняются вместе.

Фактически, эти правила и правило 2 используют свойство 3 Т-задачи.

5) После формирования допустимого решения необходимо проверить размерность базиса. Она может оказаться меньше необходимой размерности m+n- 1. Это будет означать, что формируемое базисное решение будет вырожденным. В этом случае базисное множество необходимо искусственно дополнить парами (i,j), для которых 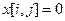. При выборе таких пар необходимо обеспечить, чтобы вводимая пара не образовывала цепочки с ранее введенными в базисное множество парами (см. свойство 8 Т-задачи).

Алгоритм формирования допустимого базисного решения Т-задачи.

Шаг 1. 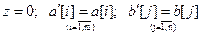;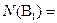Æ; матрица не определена

Шаг 2. Сформировать MUP.

Шаг 3. Выбрать из MUP первую не вычеркнутую пару (i_M, j_M).

Шаг 4.

Шаг 5.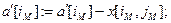

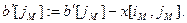
Шаг 6. Если , то все незаполненные ,().

Шаг 7. Если , то все незаполненные ,().

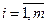Шаг 8. Из массива MUP удалить все пары (i, j), для которых на данной итерации алгоритма (шаги 3÷7) определены x [ i, j ].

Шаг 9. Если MUP еще не пуст, то переход на шаг 3.

Шаг 10. Если , то базисное множество необходимо дополнить до нужной размерности парами (i,j), для которых x [ i, j ]=0и которые не образуют цепочки с ранее введенными в базис парами (в том числе, и с теми парами, которые вводятся в базис в данном пункте).

1.15.2.3. Специальный алгоритм поиска оптимального решения Т-задачи (метод потенциалов)

Необходимо сказать, что существует не один вариант таких алгоритмов (смотри, например, Венгерский метод). Здесь будет рассмотрен лишь алгоритм, реализующий идеи симплекс-метода, так как для этого имеются все необходимые теоретические сведения.

Прежде чем изложить сам алгоритм, укажем на те его вычислительные особенности, которые отличают его от ранее рассмотренных алгоритмов симплекс-таблиц:

1) Алгоритм работает со структурой данных, не являющейся симплекс-таблицей. Основными компонентами этой структуры являются матрица перевозок x [ i,j ], базисное множество N (B _k), значения рассчитанных симплекс-разностей ∆с_ij для небазисных переменных, а также значения потенциалов , , являющихся аналогами двойственных переменных и использующихся для расчета ∆с_ij;

2) Специальным способом рассчитываются значения симплекс-разностей для небазисных компонент. При этом используется особая структура ограничений двойственной задачи (1.153). Известно (1.104), что симплекс-разности исходной задачи могут быть определены как разность правой и левой частей ограничений двойственной задачи для ее базисного решения, т.е. в данном случае:

. (1.158)

Известно также что:

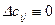для . (1.159)

Исходя из этих соотношений, можно составить следующую систему линейных уравнений для двойственных переменных:

. (1.160)

Число двойственных переменных равно числу ограничений двойственной задачи, т.е. m+n, а число уравнений системы (1.160) равно размерности базиса (m+n- 1), т.е. на единицу меньше, чем число неизвестных. Такая система решается путем задания одной из переменных произвольного значения и вычисления остальных переменных. Система уравнений (1.160) обладает таким математическим свойством, что какую бы двойственную переменную ни выбрать и какое бы значение ей ни присвоить, ее решение удовлетворяет следующему условию:

. (1.161)

Поэтому v [ i ] и w [ j ] называют потенциалами соответствующих пунктов производства и потребления (по аналогии с понятием потенциалов в электрическом поле), а сам рассматриваемый метод – методом потенциалов. Используя (1.161) и соотношение (1.158), можно после определения потенциалов следующим образом рассчитать симплекс-разности для небазисных пар (i, j):

для . (1.162)

Система (1.160), учитывая особую ее структуру, решается алгоритмически довольно просто. Для определенности первоначально полагают v [1] = 0. Исходя из этого, находят те w [ j ], которые входят в уравнения системы (1.160) вместе с v [1]. Затем по найденным w [ j ] аналогичным образом находят соответствующие v [ i ] и т.д. до тех пор, пока все и не будут определены.

3) Решаемая Т-задача не преобразуется к направлению оптимизации на максимум. Следовательно, учитывая сущность симплекс-разностей (1.74), следующим образом изменяются условия оптимальности базисного решения Т-задачи:

для (1.163)

и правила выбора столбца (i_l, j_l), вводимого в базис:

(i_l, j_l) – первая по порядку расположения в матрице перевозок пара, для которой 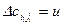, где . (1.164)

Сравните с соответствующими условиями и правилами обычного алгоритма (1.78 и 1.82).

4) Особым образом осуществляется определение пары, выводимой из базиса, и корректировка базисного решения. При этом опять используется понятие цепочки.

После добавления к базисным элементам матрицы перевозок пары (i_l, j_l) в соответствии со свойством 8 из некоторых базисных элементов сразу же образуется цепочка, замкнутая на элемент (i_l, j_l).

Алгоритм определения этой цепочки аналогичен приведенному выше. Отличие заключается лишь в том, что в п.1 алгоритма никогда не вычеркивается строка i_l, а в п.2 – столбец j_l. После завершения процедуры вычеркивания строк и столбцов матрицы перевозок выявление последовательности базисных элементов в этой цепочке осуществляется следующим образом:

-начинают с просмотра строки i_l, находят не вычеркнутый элемент (i_l, j)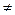(i_l, j_l); затем меняют направление поиска, ищут не вычеркнутый элемент в столбце j (пусть это будет элемент (j,k)); снова изменив направление поиска, ищут не вычеркнутый элемент в строке k, и т.д. до тех пор, пока для очередного из найденных таким образом не вычеркнутых элементов номер столбца совпадет с j_l..

- все базисные элементы цепочки последовательно нумеруются. Элементы, стоящие на нечетных местах, включаются в подмножество , а элемент на четных местах в подмножество .

Пример реализации соответствующей процедуры приведен на рис. 1.31, где базисные элементы отмечены знаком «+».

При введении (i_l, j_l) в базисное множество соответствующая перевозка x [ i_l, j_l ] в соответствии с правилом перебора допустимых базисных решений должна увеличиваться. Тогда, чтобы не выйти из области допустимых решений (см. свойство 3 Т-задачи) необходимо перевозки, стоящие на нечетных местах в цепочке, уменьшать на ту же величину, а перевозки на четных местах – увеличивать. Такое изменение будет, как и раньше, соответствовать перемещению по ребру, исходящему из крайней угловой точки прежнего базисного решения. Ограничением на перемещение, соответствующим переходу в соседнюю по ребру крайнюю точку, будет первый выход на ноль одной из уменьшающихся перевозок (т.е. одной из перевозок, входящих в подмножество ). Соответствующая пара (i_r, j_r) и будет той парой, которая из базиса выводится.

Если выходят на ноль сразу несколько перевозок, то одна из них определяется как пара

(i_r, j_r), а другие остаются в базисном множестве: базисное решение при этом будет вырожденным.

Формальные соотношения для определения (i_r, j_r) имеют следующий вид:

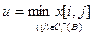, (1.165)

(i_r, j_r) – первая в множестве пара, для которой x [ i_r,j_r ] =u.

Корректировка прежнего базисного решения осуществляется в соответствии со следующими соотношениями:

; (1.166)

(1.167)

. (1.168)

Алгоритм

Шаг 1. k =1.

Шаг 2. Расчет симплекс-разностей , :

- в соответствии с N (B _k) и C [ ij ] формируется и решается система уравнений (1.160);

- рассчитываются , ,(1.162).

Шаг 3. Проверка условия оптимальности (1.163).

Если условие выполняется, то выводится оптимальное решение , и алгоритм завершает свою работу.

Шаг 4. Определение пары (i_l, j_l) в соответствии с (1.164).

Шаг 5. Определение цепочки и подмножеств и .

Шаг 6. Определение пары (i_r, j_r) в соответствии с (1.165).

Шаг 7. Корректировка базисного решения в соответствии с (1.166)÷(1.168).

Шаг 8. k:=k+ 1, переход на шаг 2.

Еще раз необходимо отметить, что исхода в соответствии со свойством 2 Т-задачи алгоритм не предусматривает.

Дата добавления: 2014-01-15