Давление света. Квантовое и волновое объяснение давления света

Одним из экспериментальных подтверждений наличия у фото­нов импульса является существование светового давления (опыты Лебедева).

Волновое объяснение (по Максвеллу): взаимодействие индуцированных токов с магнитным полем волны.

С квантовой точки зрения давление света на поверхность обусловлено тем, что при соударении с этой поверхностью каждый фотон передает ей свой импульс. Так как фотон может двигаться только со скоростью света в вакууме, то отражение света от поверхности тела следует рассматривать как процесс «переизлучения» фотонов - падающий фотон поглощается поверхностью, а затем вновь излучается ею с противоположным направлением импульса.

Рассмотрим световое давление, которое оказывает на поверхность тела поток монохроматического излучения, падающего перпендикулярно поверхности.

Пусть в единицу времени на единицу площади поверхности тела падает п фотонов. Если коэффициент отражения света от поверхности тела равен R, то Rn фотонов отражается, а (1 – R) п- поглощается. Каждый отраженный фотон передает стенке импульс, равный 2р_ф =2hv/c (при отражении импульс фотона изменяется на – р_ф). Каждый поглощенный фотон передает стенке свой импульс р_ф =hv/c. Давление света на поверхность, равно импульсу, который передают поверхности за 1 с все п фотонов:

или

, (11-12)

где I=nhv – энергия всех фотонов, падающих на единицу поверх­ности за единицу времени, т. е. интенсивность света, а w=I/c – объ­емная плотность энергии падающего излучения. Эта формула проверялась экспериментально и была подтверждена в опытах Лебедева.

4. Фотонный газ. Бозоны. Распределение Бозе − Эйнштейна.

Рассмотрим свет как совокупность фотонов, которые находятся внутри замкнутой полости с зеркальными стенками. Давление света на зеркально отражающую поверхность должно быть таким же, каким оно было бы если фотоны зеркально отражались от поверхности подобно абсолютно упругим шарикам.

Найдем давление, производимое на идеально отражающие стенки| замкнутой полости.

Для простоты предположим, что полость имеет форму куба. Ввиду изотропности излучения можно считать, что все направления движения фотонов равновероятны. Взаимодействие между фотонами отсутствует (частота их при столкновениях не меняется). Поэтому фотоны движутся подобно молекулам идеального одноатомного газа.

Давление идеального газа на стенки полости найдем из основного уравнения кинетической теории газов:

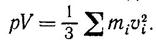
Но для фотонов m=hv_i/c², υ_i =с и поэтому mυ_i² = hv_i. Таким образом,

где W — полная энергия всех фотонов в полости, а давление на ее стенки

(11-13)

Здесь w - объемная плотность энергии излучения. Если фотоны внутри нашей полости имеют частоты от 0 до ∞, то w можно определить по формуле:

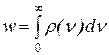(11-14)

Здесь ρ(ν) - объемная плотность энергии излучения в интервале частот от ν до ν+dν.

Функция ρ(ν) находится с помощью специального квантового распределения фотонов по энергиям (частотам), - распределения Бо­зе —Эйнштейна (Б-Э).

1. В отличие от распределения Максвелла, которое характеризует распределение частиц в пространстве скоростей (импульсов), квантовое распределение описывает энергии частиц в фазовом пространстве, образованном импульсами и координатами частиц.

2. Элементарный объем фазового пространства равен (перемножим все приращения координат):

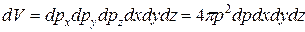(11-15)

3. Объем, приходящийся на одно состояние равен h³.

4. Число состояний dg_i излучения, находящегося в элементарном фазовом объеме в квантовой статистике получается путем деления объема (11-15) на h³:

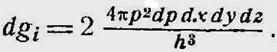
5. Распределению Б—Э подчиняются системы частиц с целым спином. Они получили название бозоны. К этим частицам относятся и фотоны. Их спин принимает целочисленные значения. Момент импульса фотона принимает значение mh/2π, где m = 1. 2,3… Функция распределения Бозе — Эйнштейна для фотонов имеет вид:

, (11-16)

где. ΔN –число фотонов в объеме dV, n_i - среднее число частиц в одном энергетическом состоянии с энергией W_i, которое называется, k — постоянная Больцмана, T – абсолютная температура. Коэффициент 2 появляется в связи с наличием двух возможных направлений по­ляризации света (левое и правое вращение плоскости поляризации).

Полное число состояний в объеме V (после интегрирования по объему и использования соотношений между импульсом фотона р и его энергией W,ν р =hv/c, W= hv):

где ν - частота, с - скорость света в вакууме.

Число фотонов с энергией от W до W + d W в объеме V:

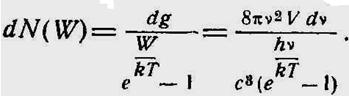(11-17)

Объемную плотность энергии излучения в интервале частот от ν до ν +dν найдем умножив (11-16) на энергию одного фотона hν:

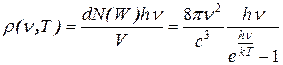. (11-18)

Давление излучения найдем по формулам (11-13), (11-14) и (11-18):

Уравнение состояния для излучения:

.

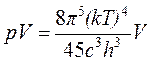Энергия излучения из объема V (закон Стефана-Больцмана):

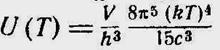
Связь между энергетической светимостью и объемной плотностью энергии излучения (следует из сопоставления формулы Планка с формулой (11-18):

R_Э(ν,Т)= (с/4)ρ(ν,Т).

Дата добавления: 2014-01-15