Метод резолюций

Методику продемонстрируем на примере. Пусть требуется доказать:

.

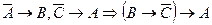Сначала поступают точно так же, как и по методике Вонга, только необходимо преобразовать клаузу таким образом, чтобы слева от символа Þ был ноль Æ:

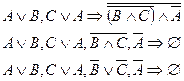
Затем из дизъюнктов составляют резолюции до тех пор, пока не получится ноль.

Выпишем по порядку все посылки и далее начнем их «склеивать». Дизъюнкты можно перебирать автоматически в соответствии с возрастанием порядковых номеров. Такая стратегия поиска нуля очень непродуктивна. К решению данной задачи можно подойти творчески.

В итоге получим:

1. АÚ В	5. (1; 4)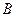
2. СÚ А	6. (2; 4) С
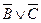
3.	7. (3; 5)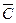
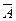
4.	8. (6; 7) Æ

Иначе, произведенные раннее преобразования, можно представить в следующем виде:

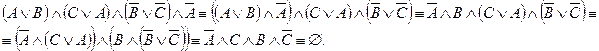
Пример: Доказать истинность заключения

(AÚB); (A«B);

(A&B).

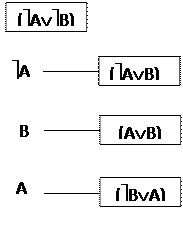1) (AÚB) - посылка;

2) (A«B)=(ùAÚB)&(ùBÚA) - посылка;

3)ù(A&B)=(ùAÚùB) –отрицание заключения;

4) K = {(AÚB); (ùAÚB); (ùBÚA); (ùAÚùB)};

5) (ùAÚùB)Ú(ùAÚB)= ùA - резольвента;

6) ùAÚ(AÚB)=B - резольвента;

7) BÚ(ùBÚA)=A - резольвента;

8) AÚùA= ÿ - пустая резольвента.

ùA

Достоинством принципа резолюции является то, что при доказательстве истинности заключения применяют только одно правило: поиск и удаление контрарных литер на множестве дизъюнктов до получения пустой резольвенты.

Алгоритм резолюции основан на том, что выводимость формулы В из множества посылок F₁; F₂; F₃;... F_n равносильна доказательству теоремы

|¾(F₁&F₂&F₃&...&F_n®B),

формулу которой можно преобразовать так:

|¾(F₁&F₂&F₃&...&F_n®B) =

|¾(ù(F₁&F₂&F₃&...&F_n)ÚB) =

|¾ù(F₁&F₂&F₃&...&F_n&(ù B)).

Следовательно, заключение В истинно тогда и только тогда, когда формула (F₁&F₂&F₃&...&F_n&(ùB))=л. Это возможно при значении “л” хотя бы одной из подформул F_i илиùB.

Для анализа этой формулы все подформулы F_i иùB должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные атомы) формируют третий дизъюнкт - резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустой дизъюнкт. Наличие пустого дизъюнкта свидетельствует о выполнении условия F₁&F₂&F₃&...&F_n&ùB=л.

Дата добавления: 2014-01-15