Линейные однородные дифференциальные уравнения. Фундаментальная система решений

Теорема (о решениях ЛОДУ).

Если - решения ЛОДУ (5.43), то их сумма 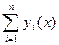также является решением этого уравнения.

Если - решение ЛОДУ (5.43), а - некоторая константа, то 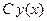также является решением этого уравнения.

Доказательство. Докажем первое утверждение теоремы, второе доказывается аналогично. Подставим сумму 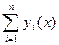в уравнение (5.43) вместо :

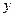n

Следствие. Если - решения ЛОДУ (5.51), а 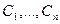- некоторые постоянные, то 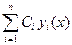также является решением этого уравнения.

Определение. Система функций называется линейно зависимой, если существуют такие константы 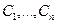(не обращающиеся в нуль одновременно), что верно тождество 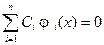. Если же тождество выполняется только когда все константы 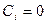, то функции называются линейно независимыми.

Определение .Фундаментальной системой решений (ф.с.р.) ЛОДУ (5.43) называется любая система линейно независимых решений 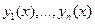этого уравнения.

Определение .Определителем Вронского (вронскианом) системы функций 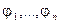называется определитель

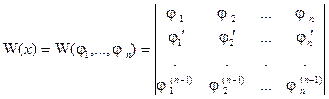. (5.44)

Теорема (о вронскиане).

Если 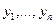- фундаментальная система решений уравнения (5.43), то

2) Если 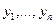- решения ЛОДУ (5.43) и 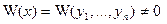хотя бы в одной точке 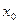, то 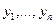- фундаментальная система решений уравнения (5.43).

Теорема (об общем решении ЛОДУ). Если 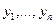- фундаментальная система решений уравнения (5.43), а 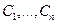- некоторые постоянные, то есть общее решение уравнения (5.43).

Пример. Определить, являются ли функции 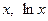линейно независимыми.

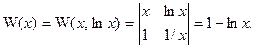
Так как 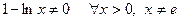, то функции линейно независимы.

Дата добавления: 2014-01-15