Теорема перемножения диаграмм направленности

Рассмотрим АР, состоящую из N элементов, заключенных в объе­ме V. Бу­дем считать, что среда, в которой находятся элементы АР и точка наблюдения, яв­ля­ется неограниченной в пространстве, линей­ной, однородной и изотропной, т.е. для нее применим принцип су­перпозиции.

Определим поле излучения решетки, создаваемое в т. М трехмерного прост-ранства, координаты которой в сферичес­кой системе определим как r, q, j.

Поле излучения n-го элемента можно определить по формуле:

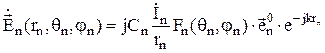, (1)

где r_n, q_n, j_n, - координаты точки М, если бы начало системы координат на­хо­дилось бы в n-ом элементе; 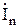- комплексная амплитуда тока (поля) в n -ом эле­менте АР; F_n(q_n, j_n,) - ДН n-го элемента; 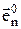- орт, характеризующий поляризацию по­ля излучения n-го элемента; С_n - амплитудный коэффициент, зависящий от вида из­лучающего элемента.

Тогда, на основании принципа суперпозиции суммарное поле, создаваемое все­ми элементами АР, будет равно:

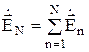. (2)

Считая, что точка наблюдения находится в дальней зоне, можно утверж­дать, что линии, соединяющие эту точку со всеми элементами АР будут парал­лель­ными, т.е. будут выполняться равенства:

q₁ = q₁ =... = q_n = q;

j₁ = j₁ =... = j_n = j;

,

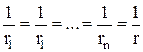т.е. можно считать, что амплитудный множитель одинаково зависит от расстоя-ния для всех элементов. Но в показателе степени (-jkr_n) приближение 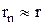- недо­пустимо, т.к. он определяет фазу поля от n-го элемента в точке наблюдения. При этом раз­ность расстояния между точкой наблюдения и двумя элементами АР мо-жет оказаться сравнимой с длиной волны, что необходимо учиты­вать при сумми-ровании полей. Кроме этого, для дальней зоны можно считать, что::

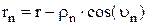, (4)

где u_n- угол между лучами r_n и г.

Учитывая выше изложенное, формулу (2) с учетом (1), (3) и (4) можно за­писать в виде:

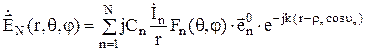. (5)

На практике АР чаще всего выполняют из одинаковых и одинако­во распо-ло­женных в пространстве излучателей. Это означает, что можно полагать:

С₁ = С₂ =... = С_n = С;

F₁(q,j) = F₂(q,j) =... = F_n(q,j) (,) = F₀(q,j), (6)

т.е. ДН у излучателей одинаковы и ориентированы в одном направле­нии.

Одинаковость поляризационной структуры поля излучателей вы­ражается в равенстве ортов:

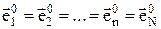. (7)

Поэтому поляризация ЭМП всей АР идентична поляризации поля, излу­чаемого каждым элементом. Это позволяет в дальнейшем рассматри­вать не векторные, а ска­лярные поля и от векторного суммирования перейти к скалярному.

Тогда выражение (5) с учетом (6) и (7) можно представить в виде:

. (8)

Из выражения (8) выпишем множители, влияющие на направленные свойст­ва АР (на распределение амплитуды напряженности поля вокруг АР):

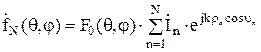. (9)

Это есть ничто иное, как ДН антенной решетки, первый сомножитель в ней - ДН оди­ноч­ного излучателя. Для выяснения физического смыс­ла второго сомножите-ля предположим, что АР состоит из ненаправ­ленных (изотропных) излучателей, т.е. F₀(q,j) = 1. При этом из (9) получаем:

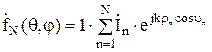, (10)

т.е. сомножитель в виде суммы представляет собой ДН этой же ре­шетки, но сос-тоя­щей из ненаправленных излучателей. Этот сомножи­тель называют множите­лем антенной решетки (множителем системы):

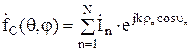. (11)

Тогда выражение (9) можно записать в следующем виде:

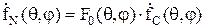. (12)

Эта запись представляет собой математическую формулировку теоремы перемно-жения ДН:

диаграмма направленности системы из идентичных и одинаково ориенти-ро­ванных в пространстве излучателей есть произведение ди­аграммы направлен­ности излучателя на множитель решетки, который представляет собой ДН той же системы, но состоящей из ненаправ­ленных излучателей.

3. Поле излучения прямолинейной эквидистантной равноамп­литудной линейно-фазной антенной решетки

Прямолинейной АР называют решетку, в которой фазовые центры излуча­те­лей распо­ложены на прямой линии - оси решетки. Расстояние между соседними излучателями возьмем одинаковым и равным d (эквидистан­тная АР).

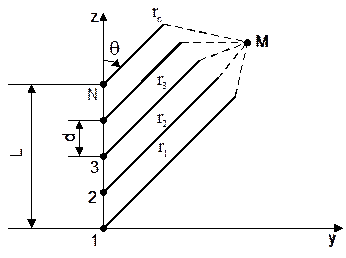
Очевидно, что конструкция такой АР является простейшей. Сле­дует пред-положить, что и множитель такой АР будет простым. Поэто­му его аналитический вывод и анализ целесообразно начать с такой АР.

Формула множителя прямолинейной антенной решетки.

Такая АР имеет направленные свойства только в одной плоскос­ти, в данном слу-чае - меридиональной. В плоскости ее направ­ленные свойства определяются толь-ко ДН отдельного излучателя. Так как все элементы расположены на одной пря-мой, которая соответст­вует оси z, то u_n = q_n = q. Кроме того, для такой АР длина радиус-вектора n-го элемента r_n и линейная координата этого элемента z_n есть од­но и то же. Тогда из (11) можем получить:

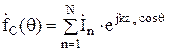. (13)

Комплексная амплитуда тока в n-ом элементе АР равна:

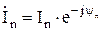, (14)

где I_n - амплитуда тока в n-ом излучателе; y_n - фаза тока в n-ом излу­ча­теле.

С учетом (14) выражение для множителя (13) примет вид:

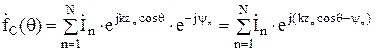. (15)

Из выражения (15), зная конструкцию АР (количество элементов АР и расстояние между ними), а также условия их возбуждения (ампли­туды и фазы токов в каж-дом элементе) можно опреде­лить множитель системы. Далее можем найти поле излучения линейной антенной решетки, подставив (15) в (8):

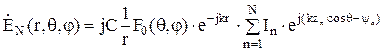. (16)

Таким образом, для определения поля излучения прямолинейной АР необ-ходимо знать координаты ее элементов, их количество и комплексную амплитуду тока возбуждения каждого элемента.

4. Множитель прямолинейной эквидистантной равноамп­литудной линейно-фазной антенной решетки

Если АР равноамплитудная, то:

I₁ = I₂ = … = I_n = I_N = 1 A. (17)

Так, как фаза тока изменяется по линейному закону, то:

y₁ = 0; y₂ = a; y₃ = 2a; … y_n = 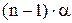(18)

где a- разность фаз токов двух соседних излучателей:

a = y₂ - y₁ = y₃ - y₂ = y_n - y_(n-1). (19)

Так, как антенная решетка эквидистантная, то координаты ее элементов можно найти из выражения:

z₁ = 0; z₂ = d; z₃ = 2d; z_n = 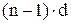(20)

С учетом (17) - (20) формула множителя (15) примет вид:

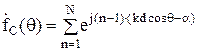. (21)

Введем обозначение так называемой обобщенной угловой коорди­наты, кото-рая есть разность фаз между полями двух соседних эле­ментов в точке наблюде-ния, находящейся под углом к оси антенной решетки:

kdcos(θ) – α = U. (22)

Тогда, подставляя (22) в (21), можем записать:

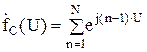. (23)

Анализ показывает, что выражение (23) - есть сумма "N" чле­нов геометричес­кой прогрессии, первый член которой равен единице, а знаменатель 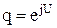. В свою очередь, эту сумму можно найти по выражению:

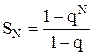. (24)

Умножая числитель и знаменатель на произведение , после преобра-зо­ва­­ний окончательно можем записать:

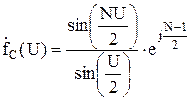. (25)

Заметим, что множитель АР состоит из двух сомножителей, пер­вый из них является амплитудной диаграммой направленности (отношение синусов), а вто-рой - фазовой диаграммой (комплексная экспонента в выражении (25). Таким об-ра­зом, амплитудный множитель из (25):

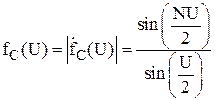. (26)

С учетом выражения для обобщенной угловой координаты (23), выра­жение (26) примет вид:

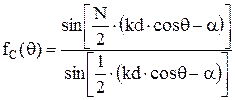. (27)

Формула (27) является по существу ненормированной ДН антенной ре­шетки с изо­тропными излучателями. Это выражение называют множите­лем решетки. Час­то пользуются нормированным множителем:

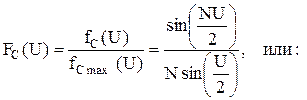
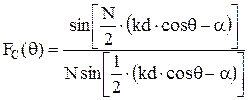. (28)

В выражениях (28) учтено, что максимальное значение множи­теля равно N.

Таким образом, используя выражения (28), можно найти множи­тель прос-тей­шей прямолинейной эквидистантной равноамплитудной ли­нейно-фазной ан­тен­ной решетки, не прибегая к сложной и трудоемкой операции суммирования, как это было в общем случае при определении множителя по выражению (15). В теории антенн получены формулы множителей и для других, неравно­ампли­туд­ных распределений токов вдоль линейной АР, существенно облегчающие нахождение их диаграмм направленности.

Дата добавления: 2014-01-15