Условие задачи

При составлении проекта работ выделено 8 событий: (0,1,2,3,4,5,6,7), которые связаны работами (i – j), где i,j 0,1,2,3…,7 и i ≠ j, например, событие 1 связано с событием 2 работой (1-2).

Исходные данные по продолжительности работ

Работа	0-1	0-2	0-3	1-2	1-3	1-4	2-3	2-4	2-5	3-4	3-5	4-5	4-6	5-6	5-7	6-7
Длит. дни

Требуется:

1. Построить сетевой график выполнения проекта.

2. Определить критический путь.

Ход выполнения:

Данная задача относится к классу задач сетевого планирования и решается методами булева программирования.

Задание 1. Построение сетевого графика выполнения проекта.

События на сетевом графике (или как говорят на графе) изображаются кружками (вершинами графа), а работы – стрелками (ориентированными дугами), показывающими связь между работами.

Так как исходные данные представлены работами, то из их анализа видно, что процесс начинается событием Ѕ₀ и заканчивается событием Ѕ₇. Все остальные события являются промежуточными.

Нарисуем график процесса, размещая события в последовательности: событие Ѕ₀ – крайне левое, Ѕ₇ – крайнее правое, если событие имеет номер i≤j,то оно изображается левее, любые события связываются одной стрелкой. С каждой стрелкой свяжем число, продолжительность работы.

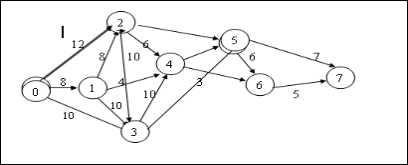
Рис.1. Сетевой график проекта.

Получим рисунок, который называется сетевым графиком проекта.

Задание 2. Определение критического пути в MS Excel.

С сетевым графиком связана таблица, которая называется матрицей инцидентностей.

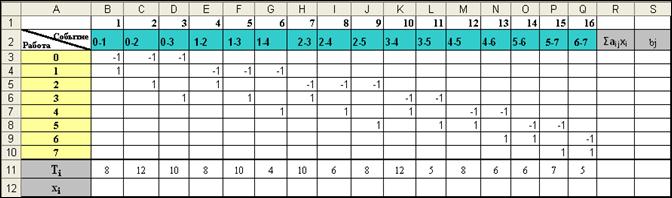
Рис. 2. Матрица инцидентностей.

Она строится следующим образом: столбцы соответствуют работам, а строки событиям. Если для дуги (i - j) начало соответствует i, а конец дуги соответствует j, то элемент матрицы в строке i будет равен -1, в строке j равен 1, а все другие элементы столбца равны 0.

1. Откройте новую книгу MS Excel и сохраните в своей папке под именем Сетевое проектирование.xls.

2. Переименуйте Лист1 в лист Матрица инцидентностей.

3. Для обеспечения проверки вводимых значений в диапазон ячеек B3:Q10 создайте список подстановки. Для этого:

· Выделите диапазон ячеек.

· Выполните команду Данные/Проверка…

· В окне Проверка вводимых значений на вкладке Параметры задайте Тип данных Список.

· В поле Источник введите значения : -1;1

4. В диапазон ячеек A11:Q11 введите продолжительность работ.

Путь – любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь L – любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим.

Полными путями являются пути:

Ѕ₀ Ѕ₃ Ѕ₅ Ѕ₇ продолжительность его 22 ед.

Ѕ₀ Ѕ₂ Ѕ₃ Ѕ₄ Ѕ₆ Ѕ₇ продолжительность 45 ед.

Критический путь имеет максимальную продолжительность.

Для вычисления критического пути введем переменные х_i = 0, если ребро не принадлежит пути и х_i =1, если принадлежит. Такие переменные называются булевыми или двоичными.

Рассмотрим функцию U(х_i)= 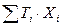, где T_i – исходные значения продолжительности работ.

По условию эта функция для критического пути должна быть максимальной. Построим систему ограничений. Все ограничения имеют вид:

,

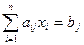где b_j = -1 – для начальной вершины,

b_j = 1 – для конечной вершины,

b_j = 0 для всех промежуточных вершин,

a_ij – элементы строки матрицы инцидентностей

Для начального события Ѕ₀ (вершина, исходящая для всех путей): -х₁-х₂-х₃= -1

Для первого события Ѕ_1: х₁-х₄- х₅- х₆=0

Для второго события Ѕ₂: х₂+х₄- х₇-х₈ –х₉=0

Для третьего события Ѕ₃: х₃+х₅+х₇- х₁₀-х₁₁=0

Для четвертого события Ѕ₄: х₆+х₈ +х₁₀-х₁₂-х₁₃=0

Для пятого события Ѕ₅: х₉+х₁₁ +х₁₂-х₁₄-х₁₅=0

Для шестого события Ѕ_6: х₁₃+х₁₄ -х₁₆=0

Для седьмого события Ѕ₇ (завершающего) х₁₅ +х₁₆=1

Начальные значения всех переменных примем равными 1.

Составим модель для поиска критического пути: Для этого:

5. В строке 12 введите переменные x_i, равные 1.

6. В столбце R рассчитайте 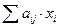, воспользовавшись функцией СУММПРОИЗ.

7. В столбец S введите ограничения b_j, учитывая, что b_j = -1 – для начальной вершины, b_j = 1 – для конечной вершины, b_j = 0 для всех промежуточных вершин.

8. В ячейке R11 рассчитайте .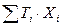

9. Сравните полученный результат с рисунком 3.

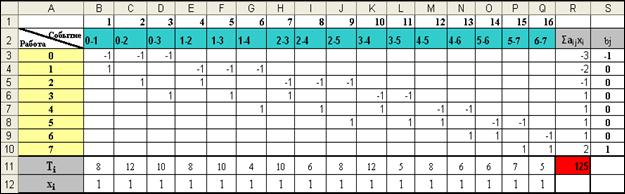
Рис. 3. Матрица инцидентностей.

10. Для того, чтобы рассчитать критический путь (максимальную продолжительность проекта), воспользуйтесь возможностями MS Excel по поиску решений. Для этого:

· Выполните команду Сервис/Поиск решений (Если данный модуль отсутствует, то предварительно установите его, выполнив команду Сервис/Надстройки/Поиск решения).

· В диалоговом окне Поиск решения установите параметры поиска решения согласно рис.4.

· Установите параметры модели – Линейная и Неотрицательные значения, щелкнув по кнопке [Параметры] диалогового окна Поиск решения.

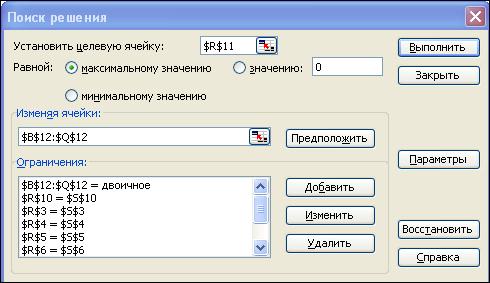
Рис. 4. Диалоговое окно Поиск решения.

Где: целевая ячейка – $R$11 (сумма произведений T_i x_i).

изменяемые ячейки – $B$12:$Q$12 (переменные х_i ).

ограничения – ячейки столбца Σa_ijx_i= bj, а также $B$12:$Q$12 = двоичное.

· Установите параметры модели – Линейная и Неотрицательные значения, щелкнув по кнопке [Параметры] диалогового окна Поиск решения.

· Щелкните по кнопке [Выполнить] и в окне Результат поиска решения установите опцию « Сохранить найденное значение» и выберите Тип отчета – Результаты.

11. По результатам поиска определите критический путь и сравните с рис. 5.

Рис. 5. Результат поиска решения.

Значение целевой функции равно 57 ед.

Таким образом, критический путь включает работы Р₀₁Р₁₂ Р₂₃ Р ₃₄ Р ₄₅ Р ₅₆Р_67.

Этот путь или подпроцесс имеет максимальную продолжительность, и работы находящиеся на нем не имеют ни каких резервов времени. Критический путь определяет полное время завершения всех работ.

Задание 3. Построение сетевого графика и определение критического пути в MS Project.

Программа MS Project предназначена для создания и управления графиками выполнения проектов на основе технологий сетевого планирования.

Окно системы приведено на рис. 6.

Рис. 6. Окно MS Project.

Слева расположена Панель консультанта (Вид /Панель инструментов/Консультант).

В рабочей области находится Диаграмма Ганта (Вид/Диаграмма Ганта), которая состоит из Панели для ввода задач (работ) и Панели протяженности работ (диаграмма выполнения проекта)

Рассмотрим выполнение проекта представленного выше.

Ход выполнения:

1. Установите дату начала выполнения проекта, выполнив команду Проект/Сведения о проекте, согласно рис. 7.

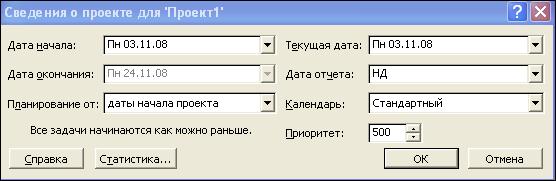
Рис. 7. Сведения о проекте.

1. Введите названия задач и их продолжительность (исходные данные) согласно рис 8. Столбцы Начало и Окончание заполнятся автоматически, столбец Предшественники заполняется перечислениями через точку с запятой номерами предшествующих работ.

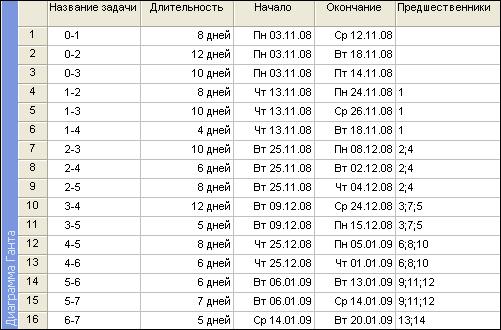
Рис. 8. Область задач диаграммы Ганта.

1. В крайнем правом столбце отражается диаграмма выполнения работ (рис. 9).

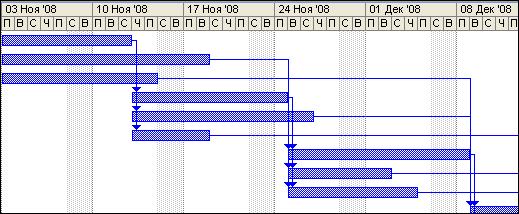
Рис. 9. Фрагмент диаграммы Ганта.

1. Рассмотрите сетевой график (Вид/Сетевой график). Работы критического пути отражены на сетевом графике красным цветом, но можно их рассмотреть отдельно, выполнив команду Проект/Фильтр /Критические задачи.
2. Определите, какова продолжительность критического пути, и какие работы он в себя включает. Сравните полученный результат с расчетами, проведенными в MS Excel. Для определения сроков выполнения проекта можно также выполнить команду Проект/Сведения о проекте (в диалоговом окне кнопка Статистика.)
3. Для того чтобы уточнить продолжительность рабочей недели, выберите на панели пункт меню Задачи , и далее пункт «Определение рабочего времени проекта».
• На первом шаге мастера укажите шаблон календаря «Стандартный».
• На втором шаге мастера укажите рабочие дни проекта.
• На третьем шаге мастера выберите пункт «Изменить рабочее время» и сделайте нерабочими днями 7.11.08, 25.12.08, 26.12.08, 01.01.09, 02.01.09, 07.01.09. Для дней 20.12.08 и 10.01.09 установите опцию Нестандартное рабочее время.
• На четвертом шаге мастера определите единицы времени.
• На пятом шаге сохраните внесенные изменения.
4. Для того чтобы связать с сетевым графиком ресурсы (например, работников и их зарплату), выберите на панели пункт меню Ресурсы, и далее перейдите по ссылке «Выбор людей и оборудования для проекта», на следующем шаге выберите опцию «Ввести ресурсы вручную». Создайте каталог трудовых ресурсов согласно рис.10. (Для всех ресурсов в диалоговом окне «Сведения о ресурсе» на вкладке «Общие» укажите тип ресурса «Трудовой»)

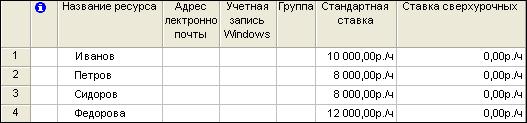
Рис. 10. Трудовые ресурсы проекта.

1. После того, как создан каталог трудовых ресурсов, нажмите на кнопку [Готово].
2. Для того чтобы связать ресурсы с задачами в окне Ресурсы перейдите по ссылке «Назначение людей и оборудования задачам». Выделите задачу 0-1 и выполните команду «Назначить ресурсы». Назначьте ресурсы задачам согласно рис.11.

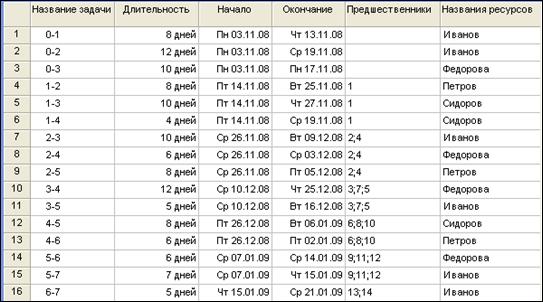
Рис. 11. Назначение ресурсов задачам.

1. После того, как ресурсы назначены, нажмите кнопку [Готово] и просмотрите лист ресурсов, выполнив команду Вид/Лист ресурсов. Обратите внимание, что Иванов и Сидоров на листе ресурсов выделены красным цветом.
2. Для того чтобы просмотреть загруженность Иванова по дням, выделите его в списке ресурсов и выполните команду Вид/График ресурсов. Обратите внимание, на какие дни приходится перегрузка данного сотрудника.
3. Для того чтобы просмотреть загруженность всех сотрудников по дням, выполните команду Вид/Использование ресурсов. На листе использования ресурсов видно, какие работы выполняет сотрудник, трудозатраты по каждой работе в отдельности и в целом по каждому сотруднику. Определите точные периоды для каждого сотрудника, когда он выполняет несколько работ одновременно и, соответственно, его рабочий день длится 16 часов.
4. Перейдите на лист Задачи и перераспределите сотрудников таким образом, чтобы не было перегрузок (в данной задаче предполагается, что все сотрудники взаимозаменяемы). Если невозможно провести оптимальное перераспределение сотрудников по задачам, то можно уменьшить трудозатраты для конкретного сотрудника по конкретному дню на листе Использование ресурсов.
5. Для добавления новых столбцов в область задач на диаграммеГанта, необходимо выделить столбец, перед которым желаете вставить новый, из контекстного меню выбрать команду Вставить столбец и в диалоговом окне «Определение столбца» указать имя вставляемого поля. Добавьте столбец Трудозатраты после поля Длительность.
6. Для определения суммарных трудовых и финансовых затрат выполните команду Проект/Сведения о проекте (в диалоговом окне кнопка Статистика).
7. Для отслеживания хода выполнения проекта выберите на панели пункт меню Отслеживание, перейдите по ссылке «Подготовка к отслеживанию хода работы над проектом», на первом шаге мастера установите опцию Нет, на втором шаге мастера выберите способ отслеживания « Всегда отслеживать путем указания процента завершения по трудозатратам» и новом поле «% завершения по трудозатратам» для работ 0-1, 0-2, 0-3 установите 100% - ное завершение. Вернитесь в окно Отслеживание и перейдите по ссылке «Проверка хода выполнения проекта». Указав любую дату, просмотрите индикатор выполнения задач проекта.
8. MS Project позволяет формировать различные виды отчетов. Для составления отчетности выберите на панели пункт меню Отчет, установите опцию «Напечатать отчет о проекте» и перейдите по ссылке «Показать отчеты». В диалоговом окне выберите категорию отчета, например, Загрузка и укажите вид отчета «Использование ресурсов». Просмотрите другие виды отчетности.

Задание 4. (самостоятельно).

При составлении проекта работ выделено 8 событий:(0,1,2,3,4,5,6,7), которые связаны работами (i –j), где i,j 0,1,2,3…,7 и i ≠ j, например событие 1 связано с событием 2 работой (1-2).Определено штатное расписание для выполнения проекта в составе:

1. Руководитель проекта (РП), стандартная ставка – 70$/день;

2. Ведущий инженер (ВИ), стандартная ставка - 60$/день;

3. Исполнитель 1 (И1), стандартная ставка - 50$/день;

4. Исполнитель 2 (И2), стандартная ставка - 50$/день;

Рабочий день исполнителя 8 часов при 5 дневной рабочей неделе.

Требуется:

1. Построить сетевой график выполнения проекта.

2. Определить критический путь.

3. Провести анализ использования ресурсов.

4. Провести анализ стоимости проекта.

Исходные данные по продолжительности работ и закрепленные работы приведены в таблице.

Дата добавления: 2014-01-15