Основні теореми диференціального числення

Вступ.

План.

Лекція 13. Застосування похідної для дослідження властивостей функцій.

Контрольні запитання.

1. Сформулюйте теореми Ферма, Ролля і Лагранжа. Якій геометричний зміст вони мають?

2. Сформулюйте необхідну і достатню умову монотонності функції на інтервалі. Поясніть на прикладах.

3. Що називається екстремумом функції? Сформулюйте необхідну і достатню умову існування екстремума функції в певній точці.

4. Яка функція на проміжку називається опуклою та угнутою?

5. При виконанні яких вимог функція буде мати точку перегину на певному інтервалі?

1. Вступ.

2. Основні теореми диференціального числення (**).

3. Зростання та спадання функцій (**).

4. Екстремуми функцій (**).

Похідна функції має широке застосування при розв’язуванні різних задач математики, фізики, техніки та економіки. Так, наприклад, за допомогою похідної можна обчислити границю функції, знайти екстремум функції, інтервали монотонності, точки перегину функції та інше.

Теорема 1 (Теоерема Ферма). Якщо диференційовна на проміжку (а; b)
функція 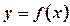досягає найбільшого або найменшого значення у внутрішній точці 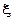цього проміжку, то похідна функції в цій точці дорівнює нулю, тобто:

Доведення.

Припустимо, для визначеності, що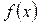набуває в точці 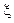найбільшого значення, тобто для всіх х з інтервалу (а; b) виконується умова: .

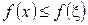За означенням похідної

,

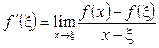причому ця границя не залежить від того, як наближається х до 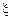— справа чи зліва.

Розглянемо відношення 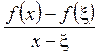. Для всіх х, достатньо близьких до точки 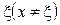, маємо:

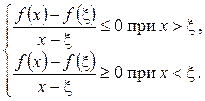
Перейдемо в останніх нерівностях до границі при . Дістанемо:

.

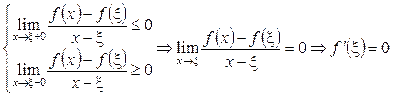Аналогічно розглядається випадок, коли функція 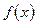набуває в точці 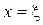найменшого значення.

Геометричний зміст теореми Ферма:геометричний зміст похідної 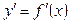являє собою кутовий коефіцієнт дотичної до кривої 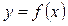, звідси рівність нулю похідної 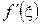геометрично озна­чає, що у відповідній точці цієї кривої дотична паралельна осі Ох.

Теорема 2 (Теорема Ролля). Якщо функція f (х):

1) неперервна на відрізку [ a; b ];

2) диференційовна на інтервалі (а; b);

3) на кінцях сегмента набуває рівних між собою значень, тобто f (a) = f (b),

то на інтервалі (а; b) існує хоча б одна точка 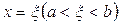, для якої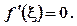

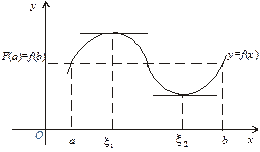
Геометричний зміст теореми Ролля: якщо крайні ординати неперервної кривої у = f (х), яка має в кожній точці дотичну, рівні, то на цій кривій знайдеться принаймні одна точка з абсцисою 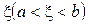, в якій дотична паралельна осі Ох.

Теорема 3 (Теорема Лагранжа). Якщо функція f (х):

1) неперервна на відрізку [ a; b ];

2) диференційовна на інтервалі (а; b),

то на інтервалі знайдеться хоча б одна точка 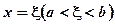, така що:

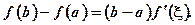
Геометричний зміст теореми Лагранжа: запишемо формулу у іншому вигляді:

.

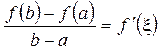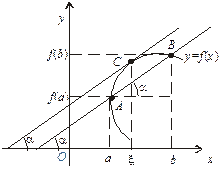
З малюнка бачимо, що величина 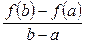є тангенсом кута 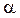нахилу хорди, що проходить через точки А і В графіка функції
у = f (х) з абсцисами а і b.

Водночас, 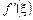— тангенс кута нахилу дотичної до кривої у точці С з абсцисою 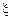. Таким чином: якщо для всіх точок кривої у = f (х) існує дотична, то на цій кривій знайдеться точка з абсцисою 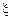, в якій дотична паралельна хорді АВ, що сполучає точки А і В.

Теорема 3 (Теорема Коші). Якщо f (x) і 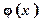дві функції:

1) неперервні на відрізку [ a; b ];

2) диференційовні на інтервалі (а; b);

3) 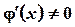для ,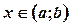

то на інтервалі (а; b) знайдеться хоча б одна точка 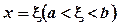, така що

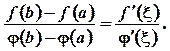
Дата добавления: 2014-01-15