
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений
|
|
|
|
Главные, побочные и грузовые коэффициенты системы канонических уравнений (16.4) по смыслу представляют собой перемещения в основной системе по направлению реакций в удалённых связях от неизвестных метода сил, численно равных единице, и от заданной нагрузки. Эти перемещения можно вычислить по формуле Мора, если известны внутренние усилия в основной системе метода сил от Xi = 1, Xj = 1 и от заданного силового воздействия, в грузовом и единичном состояниях (см. п. 11.2 второй части настоящего курса лекций). Следует иметь ввиду, что при вычисления главного коэффициента dii грузовое и единичное состояния совпадают.
 (16.5)
(16.5)
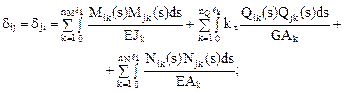 (16.6)
(16.6)
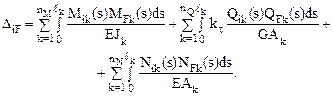 (16.7)
(16.7)
В соотношениях (16.5)–(16.7):
Mik(s), Qik(s), Nik(s), Mjk(s), Qjk(s), Njk(s) – функции, описывающие изменение внутренних усилий (изгибающих моментов, поперечных и продольных сил) на k-ом грузовом участке, от действия Xi = 1, Xj = 1 в основной системе метода сил;
MFk(s), QFk(s), NFk(s) – функции, описывающие изменение внутренних усилий на k-ом грузовом участке от заданной нагрузки, в основной системе метода сил;
kt – коэффициент, учитывающий неравномерность распределения касательных напряжений по высоте поперечного сечения на соответствующем грузовом участке;
ℓk – длина k-го грузового участка для конкретного усилия;
nM, nQ, nN – число грузовых участков, в пределах которых закон изменения изгибающих моментов, поперечных и продольных сил описывается одним аналитическим выражением.
В рамных и балочных системах доля перемещений, определяемых деформациями сдвига и растяжения-сжатия, незначительна по сравнению с долей перемещений, вызываемых изгибными деформациями (см. п. 11.3 второй части настоящего курса лекций). В этом случае, с точностью достаточной для инженерных расчётов, определение коэффициентов dii, dij и DiF в основной системе метода сил может быть произведено только с учётом деформаций изгиба, т.е.
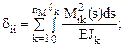 (16.8)
(16.8)
 (16.9)
(16.9)
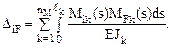 (16.10)
(16.10)
Определённые интегралы выражений (16.5)–(16.7) чаще всего вычисляются по формуле Симпсона (см. п. 11.4 второй части настоящего курса лекций). При ступенчато-переменных значениях жёсткостей поперечных сечений EJk, GAk, EAk и при действии на сооружение произвольных сосредоточенных сил и моментов, а также распределённых нагрузок с постоянной интенсивностью, эта формула даёт точные значения определённых интегралов, входящих в формулу Мора. В случае, когда одна или обе подынтегральных функции линейны, вычисление вышеупомянутых определённых интегралов можно произвести, используя правило Верещагина.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!