Коды с коррекцией искажений

Если сигналы составлены таким образом, что один отличается от другого не менее чем тремя элементами, то при искажении одного элемента какого-либо сигнала можно установить, какой сигнал был первоначально послан, т.к. искаженный в одном элементе сигнал будет отличаться от посланного одним элементом, а от всех остальных – минимум двумя элементами.

Это дает возможность скорректировать искаженный в одном элементе сигнал и реализовать его как правильный.

В качестве примера рассмотрим систему пятиэлементных кодовых комбинаций, отличающихся друг от друга не менее чем 3 элементами

1) 11010

2) 01001

3) 00110

4) 10101

Пусть принят сигнал, соответствующий кодовой комбинации 01011. Такой комбинации в списке нет, следовательно это искаженный сигнал. Он отличается от первой комбинации двумя элементами, от второй – одним элементом, от третьей – тремя и от четвертой – четырьмя элементами.

Вывод: скорее всего это сигнал 2, искаженный в одном элементе.

Тогда энтропия кода:

Справка. При равных вероятностях P _i всех n состояний энтропия равна

но , тогда

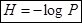- формула Хартли

Сигнал (символ) любого числового кода на все сочетания несет информацию

где В – основание системы счисления, n – число элементов в сигнале (символе).

Избыточность кода D определяется выражением

(6)

Н – энтропия данного кода, имеющего N сигналов

Н =log N

Минимальное число элементов сигнала, необходимое для образования N комбинаций, как и в рассматриваемом коде

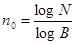
(7)

Иначе

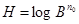(8)

H _max – максимальное число сигналов (символов, комбинаций), которые можно организовать из элементов данного кода (фактически это код на все сочетания)

(9)

где n – число элементов сигнала (символа) данного кода.

Тогда

(10)

Отметим, что, как правило, если n₀ получается дробным, его округляют до целого числа в большую сторону.

Таким образом, безошибочные передачи при наличии помех возможны лишь теоретически.

Обеспечение передачи информации с весьма малой вероятностью ошибки и достаточно высокой эффективностью возможно лишь при кодировании чрезвычайно длинных последовательностей знаков. На практике степень достоверности и эффективности ограничивается двумя факторами: размерами и стоимостью аппаратуры кодирования и декодирования и временем задержки передаваемого сообщения.

Литература

1. Дмитриев В.И. Прикладная теория информации. Учеб. для студ. вузов по спец. «Автоматизированные системы обработки информации и управления».-М.:Высш.шк., 1989.-320 с.: ил.
2. Вострокнутов Н.Г., Евтихиев Н.Н. Информационно-измерительная техника. Учеб.пособие для вузов по специальности «Информационно-измерительная техника». М., Высш.шк., 1977.-232с.: ил.
3. Бондарев В.Н., Трестер Г., Чернега В.С. Цифровая обработка сигналов: методы и средства. Учебное пособие для вузов.- Севастополь. Изд-во СевГТУ, 1999.-398 с.: ил.
4. Орнатский П.П. Теоретические основы информационно - измерительной техники. Изд. «Вища школа», 1976, 432 с.
5. Таланчук П.М., Рущенко В.Т. основы теории и проектирования измерительных приборов. Учеб. пособие. – К. Вища школа Головное изд-во, 1989.- 454 с.: ил.
6. Координатные измерительные машины и их применение /В.-А.А.Гапшис, А.Ю.Каспарайшис, М.Б.Модестов и др.-М.: Машиностроение, 1988.- 328 с.: ил.
7. Цапенко Информационно-измерительная техника
8. Вальков Контроль в ГПС
9. Земеко Г.Г., Савельев В.А. Средства измерения линейных размеров с использованием ОКГ. М.:Машиностроение, 1977 г.
10. Справочник по лазерной технике. К.: Технiка, 1978. Под. ред. Байбородина.
11. Иванов Измерительные приборы в машиностроении. 1981.

Дата добавления: 2014-01-15