Поле излучения линейной антенны

Как следует из электродинамики, задача определения поля излучения по за­данному закону распределения токов (зарядов) сводится к решению уравнения за­паз­дывающих потенциалов, выраженного через вектор Герца:

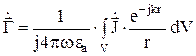, (2)

где 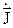- вектор плотности тока проводимости;.

Интегрирование в (2) ведется по объему V, в котором существует ток проводи-мос­ти.

В свою очередь, напряженность электрических и магнитных полей, создава­е­мых проводником с током можно найти через вектор Герца, пользуясь известны­ми выражениями:

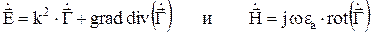, (3)

причем дифференцирование в (3) производится по координатам точки наб­лю­дения.

Выразим первое уравнение (3) в сферической системе координат. При этом учтем, что нас интересуют характеристики поля в дальней зоне антенны, (где 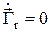) и то, что в точке наблюдения нет собственных источников поля

(grad div 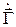=0), тогда его можно представить в следующем виде:

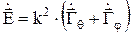, (4)

где 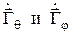- составляющие вектора Г, направленные по ортам 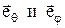сфе­рической системы координат.

Считая провод прямолинейным, круглого сечения, совместим центр пря­моу­гольной системы координат XYZ с серединой провода, как это показано на рисунке. Так как ток течет вдоль провода, то плотность тока в каждом, произвольно взя­том сечении провода равна: 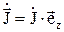и второй сомножитель выражения (2) бу­дет иметь следующий вид:

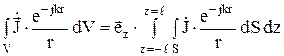, (5)

где 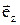- орт, определяющий направление провода вдоль оси OZ.

При интегрировании по малому поперечному сечению провода в (5), когда ко­ордината z имеет фиксированное значение, можно считать:

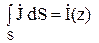. (6)

Для дальней зоны расстояние до точки наблюдения определяется следую­щим образом:

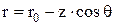, (7)

т.е. точка М видна из разных участков провода под одним и тем же углом θ.

Из рисунка видим, что в сферической системе координат при данном расположе­нии провода и вследствие его осевой симметрии относительно оси OZ, вектор 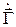име­ет единственную составляющую 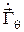. Поэтому, с учетом (5), (6) и (7), выраже­ние (2) примет вид:

. (8)

Так как , то напряженность поля, создаваемая проводом согласно (4), определяется так:

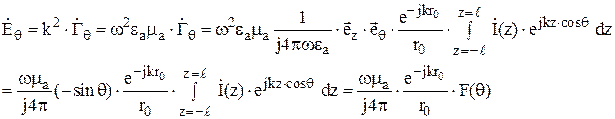, (9)

где F(θ) – диаграмма направленности линейной антенны:

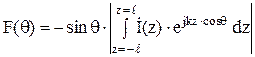. (10)

Уравнения (9) и (10) позволяют сделать следующие выводы:

- излучающий провод создает в дальней зоне электромагнитное поле, имею­щее составляющие 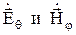, значения которых зависят от угла θ и не зависят от уг­ла φ, т.е. в распределении поля вокруг провода с круглым сечением будет су-щест­вовать осевая симметрия;

- фазовый фронт волны представляет собой сферу, имеющую центр в гео­мет­ри­ческом центре провода. Это и есть фазовый центр антенны;

- выражение (10) характеризует направленные свойства провода и предс­тав­ляет собой запись теоремы перемножения. Первый сомножитель - ДН элемента неп­рерывной АР (вибратора Герца) F₀(θ) = - sinθ; второй - множитель непрерыв­ной прямолинейной АР с законом распределения тока вдоль нее .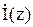

Зная длину провода 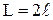, а также закон распределения тока по нему 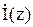, мож­но определить амплитуду напряженности поля излучения:

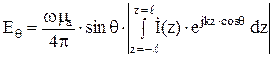. (11)

Дата добавления: 2014-01-15