
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: двухфакторный дисперсионный анализ
|
|
|
|
1o. Математическая модель метода
В двухфакторном дисперсионном анализе изучается влияние двух независимых факторов А и В на изменчивость признака Х нормально распределенной генеральной совокупности. При этом фактор А может действовать на т своих уровнях: А 1, А 2, …, Ап, а фактор В – на l уровнях: В 1, В 2, …, Вl. Далее будем рассматривать случай, когда на каждом совмещенном уровне АiBj производится выборка одинакового объема п, и все выборки на этих уровнях независимы. Выборочные данные можно представить таблицей:
 В
А В
А
| В 1 | … | Вj | … | Bl |
| A 1 … Ai … Am | x 111 … x 11 n … xi 11 … xi 1 n … xm 11 … xm 1 n | … … … … … | x 1 j 1 … x 1 jn … xij 1 … xijn … xmj 1 … xmjn | … … … … … | x 1 l 1 … x 1 ln … xil 1 … xiln … xml 1 … xmln |
Т.о., объем объединенной выборки п * = l · m · n. Объединенная выборка производится из генеральной совокупности, обладающей изучаемым признаком, задаваемым нормально распределенной случайной величиной, т.е. Х ~ N (a; s), причем математическое ожидание М (Х) = а и стандартное отклонение s считаются неизвестными. В двухфакторном дисперсионном анализе для выборочных значений признака xijk принимается за основу линейная вероятностная схема: xijk =  + a i + b j + g ij + e ijk, где xijk – k -йрезультат наблюдения на i -м уровне фактора А и на j -м уровне фактора В,
+ a i + b j + g ij + e ijk, где xijk – k -йрезультат наблюдения на i -м уровне фактора А и на j -м уровне фактора В,  – несмещенная оценка М (Х) = а, a i – эффект действия фактора А на его i -м уровне, b j – эффект действия фактора В на его j -м уровне, e ijk – нормальная случайная величина с нулевым математическим ожиданием на каждом уровне, обусловленная влиянием неучтенных факторов и условий.
– несмещенная оценка М (Х) = а, a i – эффект действия фактора А на его i -м уровне, b j – эффект действия фактора В на его j -м уровне, e ijk – нормальная случайная величина с нулевым математическим ожиданием на каждом уровне, обусловленная влиянием неучтенных факторов и условий.
Ограничения метода для рассматриваемой модели:
Ø уровней (градаций) действия каждого фактора должно быть не менее двух;
Ø объем выборки на каждом совмещенном уровне действия факторов должен быть не менее двух;
Ø каждой градации одного фактора должно соответствовать одинаковое число градаций другого фактора;
Ø должно выполняться равенство дисперсий всех генеральных совокупностей, к которым принадлежат полученные независимые выборки по всем совмещенным уровням действия факторов.
В двухфакторном дисперсионном анализе возможны 3 комплекса гипотез в связи с возможным влиянием на признак только фактора А, только фактора В, а также совместного влияния обоих факторов.
1- й комплекс гипотез.
Основная гипотеза НА: различие признака на разных уровнях фактора А является не более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
Альтернативная гипотеза 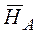 : различие признака на разных уровнях фактора А является более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
: различие признака на разных уровнях фактора А является более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
2- й комплекс гипотез.
Основная гипотеза НВ: различие признака на разных уровнях фактора В является не более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
Альтернативная гипотеза 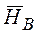 : различие признака на разных уровнях фактора В является более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
: различие признака на разных уровнях фактора В является более выраженным, чем случайные различия этого признака внутри каждого уровня этого фактора.
3- й комплекс гипотез.
Основная гипотеза НАВ: влияние фактора А на признак на разных уровнях фактора В одинаково, и наоборот.
Альтернативная гипотеза 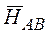 : влияние фактора А на признак на разных уровнях фактора В различно, и наоборот.
: влияние фактора А на признак на разных уровнях фактора В различно, и наоборот.
Кроме того могут рассматриваться 3 модели в зависимости от того, детерминированы уровни факторов или эти уровни – результат случайного отбора.
Модель I: выявляется действие факторов с детерминированными уровнями (например, при исследовании качества продукции один из факторов – станки, тогда фактор имеет детерминированные уровни, если в наблюдении участвуют все станки или конкретно заданные станки).
Модель II: выявляется действие факторов, уровни которых – результат случайного отбора (например, при исследовании качества продукции для наблюдения случайно отобрана часть станков).
Модель III: фактор А соответствует 1-й модели, а фактор В – 2-й модели.
2o. Расчетные формулы и схема дисперсионного анализа
Для ускорения расчетов рекомендуется использовать следующую схему проведения двухфакторного дисперсионного анализа:
1) Найти суммы и суммы квадратов наблюдаемых значений для каждого совмещенного уровня АiBj соответственно: Tij = 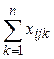 , Pij =
, Pij =  , где п – число наблюдений на каждом совмещенном уровне факторов А, имеющем т уровней действия, и В, имеющего l уровней действия; объем объединенной выборки равен п * = lтп.
, где п – число наблюдений на каждом совмещенном уровне факторов А, имеющем т уровней действия, и В, имеющего l уровней действия; объем объединенной выборки равен п * = lтп.
2) Найти суммы полученных значений Tij для каждого уровня фактора А: ui = 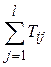 , и для каждого уровня фактора В: vj =
, и для каждого уровня фактора В: vj = 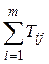 .
.
3) Найти сумму Pij по всем совмещенным уровням: w = 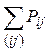 .
.
4) Найти суммы: u = 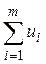 =
=  , a =
, a = , b =
, b =  и c =
и c =  .
.
5) Найти общую вариативность признака Q = w – · u 2.
· u 2.
6) Найти A -факторную вариативность признака Q 1 = 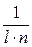 · a –
· a –  · u 2.
· u 2.
7) Найти B -факторную вариативность признака Q 2 =  · b –
· b –  · u 2.
· u 2.
8) Найти остаточную вариативность признака Q 4 = w – 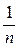 · c.
· c.
9) Найти вариативность признака, обусловленную совместным воздействием на него факторов А и В: Q 3 = Q – Q 1 – Q 2 – Q 4.
10) Найти несмещенные точечные оценки А- факторной s 12, В- факторной s 22, АВ -факторной s 32 и остаточной s 42 дисперсий: s 12 = Q 1/(т – 1); s 22 = Q 2/(l – 1); s 32 = Q 3/[(l – 1)·(m – 1)]; s 42 = Q 4/(п * – l · т).
11) Используя ниже приведенную таблицу, найти наблюдаемые K н и для заданного уровня значимости a критические значения K кр критерия проверки соответствующих гипотез с правосторонней критической областью и сделать заключение о значимости влияния соответствующих факторов на исследуемый признак генеральной совокупности:
| Модели | Н 0 | K н | K кр |
| Модель I (уровни факторов А и В детерминированы) | НА НВ НАВ | s 12/ s 42 s 22/ s 42 s 32/ s 42 | F a(k 1 = m – 1; k 2 = n * – lm) F a(k 1 = l – 1; k 2 = n * – lm) F a(k 1 = (l –1)·(m –1); k 2 = n * – lm) |
| Модель II (уровни факторов А и В случайны) | НА НВ НАВ | s 12/ s 32 s 22/ s 32 s 32/ s 42 | F a(k 1 = m – 1; k 2 = (l –1)·(m –1)) F a(k 1 = l – 1; k 2 = (l –1)·(m –1)) F a(k 1 = (l –1)·(m –1); k 2 = n * – lm) |
| Модель III (уровни фактора А детерминированы, а В – случайны) | НА НВ НАВ | s 12/ s 42 s 22/ s 32 s 32/ s 42 | F a(k 1 = m – 1; k 2 = n * – lm) F a(k 1 = l – 1; k 2 = (l –1)·(m –1)) F a(k 1 = (l –1)·(m –1); k 2 = n * – lm) |
Пример. Каждый из 3-х менеджеров на тестовом занятии предложил свой проект модернизации двух конкретных предприятий. Четыре эксперта независимо друг от друга выставили оценки разработанным проектам по 10-балльной шкале, принимая во внимание готовность предприятий к предлагаемой модернизации:
| 1-е предприятие | 2-е предприятие | |
| 1-й менеджер | 6; 9; 4; 8 | 7; 8; 8; 9 |
| 2-й менеджер | 5; 5; 7; 7 | 8; 7; 6; 7 |
| 3-й менеджер | 6; 6; 8; 6 | 7; 8; 8; 8 |
В предположении, что требования к дисперсионному анализу выполняются, требуется установить на уровне значимости a = 0,05 влияние различия этих проектов и уровня готовности предприятий к предложенной модернизации на оценки экспертов.
Решение. В качестве фактора А будем рассматривать менеджеров, а в качестве фактора В – предприятия, для которых разработаны проекты модернизации. Уровни обоих факторов детерминированы. Число уровней (градаций) А -фактора т = 3, а В -фактора l = 2. На каждом совмещенном уровне АiBj имеем п = 4 оценки; объем объединенной выборки п * = lтп = 2·3·4 = 24.
На 5%-м уровне значимости следует проверить следующие комплексы гипотез:
1. Основная гипотеза НА: различие оценок экспертов для трех тестируемых менеджеров является не более выраженным, чем случайные различия этих оценок для каждого из менеджера в отдельности, или другими словами, все три проекта практически равноценны. Альтернативная гипотеза 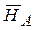 : различие между проектами значимо.
: различие между проектами значимо.
2. Основная гипотеза НВ: различие оценок проектов экспертами для двух предприятий в целом является не более выраженным, чем случайные различия этих оценок для каждого предприятия в отдельности, или, другими словами, готовность предприятий к предлагаемой модернизации практически одинакова. Альтернативная гипотеза  : уровень готовности предприятий к предлагаемой модернизации существенно различен.
: уровень готовности предприятий к предлагаемой модернизации существенно различен.
3. Основная гипотеза НАВ: во всех проектах в одинаковой степени отражено различие готовности предприятий к предлагаемой модернизации. Альтернативная гипотеза 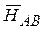 : в проектах в разной степени выражено различие готовности предприятий к предлагаемой модернизации.
: в проектах в разной степени выражено различие готовности предприятий к предлагаемой модернизации.
Составляем расчетную таблицу:

| В 1 | В 2 | ui = 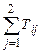 ; ui 2 ; ui 2
|
| А 1 | Т 11 = 6 + 9 + 4 + 8 = 27
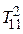 = 272 = 729
Р 11 = 62 + 92 + 42 + 82 = 197 = 272 = 729
Р 11 = 62 + 92 + 42 + 82 = 197
| Т 12 = 7 + 8 + 8 + 9 = 32
 = 322 = 1024
Р 12 = 72 + 82 + 82 + 92 = 258 = 322 = 1024
Р 12 = 72 + 82 + 82 + 92 = 258
| u 1 = Т 11 + Т 12 = 59 u 12 = 592 = 3481 |
| А 2 | Т 21 = 5 + 5 + 7 + 7 = 24
 = 242 = 576
Р 21 = 52 + 52 + 72 + 72 = 148 = 242 = 576
Р 21 = 52 + 52 + 72 + 72 = 148
| Т 22 = 8 + 7 + 6 + 7 = 28
 = 282 = 784
Р 22 = 82 + 72 + 62 + 72 = 198 = 282 = 784
Р 22 = 82 + 72 + 62 + 72 = 198
| u 2 = Т 21 + Т 22 = 52 u 12 = 522 = 2704 |
| А 3 | Т 31 = 6 + 6 + 8 + 6 = 26
 = 262 = 676
Р 31 = 62 + 62 + 82 + 62 = 172 = 262 = 676
Р 31 = 62 + 62 + 82 + 62 = 172
| Т 32 = 7 + 8 + 8 + 8 = 31
 = 312 = 961
Р 32 = 72 + 82 + 82 + 82 = 241 = 312 = 961
Р 32 = 72 + 82 + 82 + 82 = 241
| u 3 = Т 31 + Т 32 = 57 u 12 = 572 = 3249 |
vi = 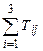 ; vi 2 ; vi 2
| v 1 = Т 11+ Т 21+ Т 31 = 77 v 12 = 772 = 5929 | v 2 = Т 12+ Т 22+ Т 32 = 91 v 12 = 912 = 8281 |
Используя данные, полученные в расчетной таблице, находим:
u = u 1 + u 2 + u 3 = 59 + 52 + 57 = 168;
a = u 12 + u 22 + u 32 = 3481 + 2704 + 3249 = 9434;
b = v 12 + v 22 = 5929 + 8281 = 14210;
c =  = 729 + 1024 + 576 + 784 + 676 + 961 = 4750;
= 729 + 1024 + 576 + 784 + 676 + 961 = 4750;
w =  = 197 + 258 + 148 + 198 + 172 + 241 = 1214.
= 197 + 258 + 148 + 198 + 172 + 241 = 1214.
Находим общую вариативность оценок экспертов Q = w – · u 2 = 1214 – 1682/24 = 38.
· u 2 = 1214 – 1682/24 = 38.
Находим вариативность оценок, обусловленную действием фактора А: Q 1 = 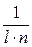 · a –
· a –  · u 2 = 9434/8 – 1682/24 = 3,25.
· u 2 = 9434/8 – 1682/24 = 3,25.
Находим вариативность оценок, обусловленную действием фактора В: Q 2 =  · b –
· b –  · u 2 = 14210/12 – 1682/24 ≈ 8,17.
· u 2 = 14210/12 – 1682/24 ≈ 8,17.
Находим остаточную вариативность оценок Q 4 = w – 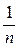 · c = 1214 – 4750/4 = 26,5.
· c = 1214 – 4750/4 = 26,5.
Находим вариативность оценок, обусловленную взаимодействием факторов А и В: Q 3 = Q – Q 1 – Q 2 – Q 4 = 38 – 3,25 –8,17 – 26,5 = 0,08.
Находим несмещенные точечные оценки А- факторной s 12, В- факторной s 22, АВ -факторной s 32 и остаточной s 42 дисперсий: s 12 = Q 1/(т – 1) = 3,25/2 = 1,625; s 22 = Q 2/(l – 1) = 8,17; s 32 = Q 3/[(l – 1)·(m – 1)] = 0,04; s 42 = Q 4/(п * – l · т) = 26,5/18 ≈ 1,47.
Находим наблюдаемые значения статистического критерия проверки соответствующих основных гипотез:
Ø для гипотезы НА: K н1 = s 12/ s 42 = 1,625/1,47 ≈1,1;
Ø для гипотезы НВ: K н2 = s 22/ s 42 = 8,17/1,47 ≈ 5,56;
Ø для гипотезы НАВ: K н3 = s 32/ s 42 = 0,04/1,47 ≈ 0,03.
По табличным значениям критических точек F- критерия Фишера-Снедекора для уровня значимости a = 0,05 и соответствующим степеням свободы: K кр1 = F 0,05(k 1 = 2; k 2 = 18) = 3,55; K кр2 = F 0,05(k 1 = 1; k 2 = 18) = 4,41; K кр3 = F 0,05(k 1 = 2; k 2 = 18) = 3,55.
Поскольку K н1 < K кр1, то гипотеза НА принимается, т.е. все три проекта практически равноценны.
Поскольку K н2 > K кр2, то гипотеза НВ отклоняется, и принимается альтернативная гипотеза  : уровень готовности предприятий к предлагаемой в проектах модернизации существенно различен.
: уровень готовности предприятий к предлагаемой в проектах модернизации существенно различен.
Поскольку K н3 < K кр3, то гипотеза НАВ принимается, т.е. во всех проектах в одинаковой степени отражено различие готовности предприятий к предлагаемой модернизации (как следует из оценок экспертов, во всех проектах не учтено отличие этой готовности).
 |
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1754; Нарушение авторских прав?; Мы поможем в написании вашей работы!