Использование симметричной основной системы метода сил

Если для расчёта рамы, имеющей вертикальную ось симметрии (рис. 18.1,а) на произвольное воздействие (силовое, температурное или кинематическое) использовать несимметричную основную систему метода сил, показанную на рис. 18.1,б, то этот расчёт сведётся к решению полной системы четырёх алгебраических неоднородных уравнений с четырьмя неизвестными Х₁, Х₂, Х₃, Х₄. Эта система уравнений для рассматриваемой задачи примет вид:

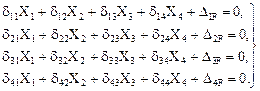(18.1)

Приняв для расчёта рамы симметричную основную систему (рис. 18.1,в), мы будем иметь дело с обратносимметричными (Х₁ и Х₃) и симметричными неизвестными (Х₂ и Х₄). От единичных значений этих неизвестных эпюры внутренних усилий будут обратносимметричными или симметричными. В частности, для рассматриваемой рамы, учитывая только деформации изгиба её элементов, в основной системе будем иметь: эпюры М₁ и М₃, соответственно, от Х₁ = 1 и Х₃ = 1 – обратносимметричными, эпюры М₂ и М₄ от Х₂ = 1 и Х₄ = 1 –симметричными.

Сопрягая обратносимметричные эпюры изгибающих моментов М₁ и М₃ с симметричными – М₂ и М₄, получим:

,

,

,

.

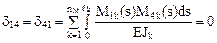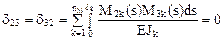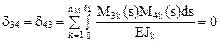С учётом нулевых значений вышеперечисленных побочных коэффициентов система канонических уравнений метода сил (18.1) распадётся на две независимых друг от друга системы двух уравнений с двумя неизвестными, причём первая из этих систем уравнений будет содержать только обратносимметричные неизвестные, а вторая – только симметричные.

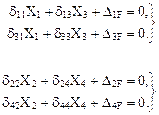
Дата добавления: 2014-01-15