Основные линии и плоскости эллипсоида

Существует определение, что эллипсоид — геометрически правильное тело, образованное вращением эллипса РЕ₁Р₁Е вокруг малой оси РР₁, (рис. 3.1). Малая ось эллипсоида РР₁ — геометрическая ось вращения Земли, а центр эллипсоида О — центр тяжести Земли. Малая ось эллипсоида в пересечении с поверхностью эллипсоида образует две точки, называемые п ол ю с а м и, один из которых Р — северный, а другой Р₁ — южный. Любое сечение поверхности эллипсоида плоскостью, перпендикулярной оси вращения, представляет собой окружность, а сечение, не перпендикулярное оси вращения, — эллипс.

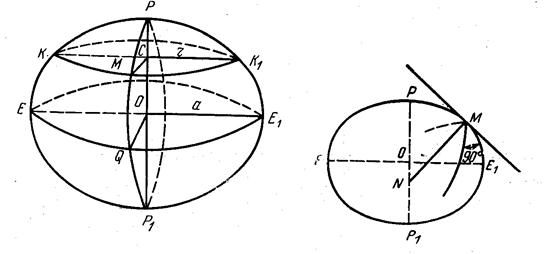
Рис. 3.1 Рис. 3.2

Плоскость ЕОЕ₁, перпендикулярная к оси вращения эллипсоида и проходящая через его центр, называется п л о с к о с т ь ю э к в а т о р а. Линия сечения поверхности эллипсоида плоскостью экватора называется э к в а т о р о м. Экватор — окружность, радиус которой равен большой полуоси эллипсоида ОЕ₁, = ОЕ = OQ = а.

Сечения поверхности эллипсоида плоскостями, параллельными плоскости экватора, а следовательно, перпендикулярными к оси вращения, называется п а р а л л е л я м и, которые представляют собой также окружности определенного радиуса r = КС = СК₁ = СМ.

Плоскости, проходящие через ось вращения эллипсоида, называются меридианными плоскостями, а сечения ими поверхности эллипсоида — г е о д е з и ч е с к и м и м е р и д и а н а м и. Очевидно, что все меридианные плоскости перпендикулярны плоскости экватора и любой меридиан — эллипс, который своим вращением образует эллипсоид.

Если через точку М, лежащую на поверхности эллипсоида, провести касательную плоскость (рис. 3.2), то прямая МN, проходящая через данную точку, перпендикулярная к касательной плоскости, называется н о р м а л ь ю к поверхности эллипсоида в точке М.

В точках, расположенных в северной половине эллипсоида, нормали пересекают ось вращения эллипса южнее его центра, а в точках, расположенных в южной половине, — севернее его центра.

Очевидно, что нормали точек экватора лежат в плоскости экватора, а на полюсах — совпадают с осью вращения.

Все плоскости, проходящие через нормаль данной точки, называются нормальными плоскостями, а линии пересечения нормальными плоскостями поверхности эллипсоида — нормальными сечениями. Следовательно, меридианы и экватор являются нормальными сечениями.

Всякое другое сечение эллипса плоскостью, не проходящей через нормаль, называется наклонным. Следовательно, параллели — наклонные сечения.

Нормальная плоскость в точке М, перпендикулярная к плоскости меридиана точки М, называется плоскостью первого вертикала. Сечение плоскостью первого вертикала поверхности эллипсоида называется первым вертикалом.

Меридиан и первый вертикал называются главным и нормальными сечениями.

Угол, образованный в точке эллипсоида М (рис. 3.3) нормальным сечением МК и геодезическим меридианом точки М — РМР₁ называется геодезическим азимутом А направления МК.

Счет азимутов ведут по ходу часовой стрелки от северного направления меридиана до данного направления. Азимуты могут изменяться от 0до 360°.

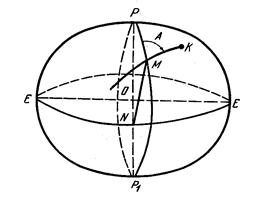
Рис. 3.3

Дата добавления: 2014-01-15