Астрономические координаты

Положение точки на геоиде в системе астрономических координат определяется широтой φ и долготой λ.

Астрономической широтой точки М называется угол φ, образованный направлением отвесной линии в данной точке с плоскостью экватора.

Астрономической долготой точки М называется двугранный угол между плоскостями начального и астрономического меридиана данной точки (плоскость астрономического меридиана — плоскость, проходящая через отвесную линию в этой точке и параллельная оси мира).

Астрономическим азимутом направления МК — α называется угол в точке М, образованный направлением астрономического меридиана и сечением геоида отвесной плоскостью, проходящим через точки М и К.

Для уяснения разницы между геодезическими и астрономическими координатами обратимся к рис. 5.2.

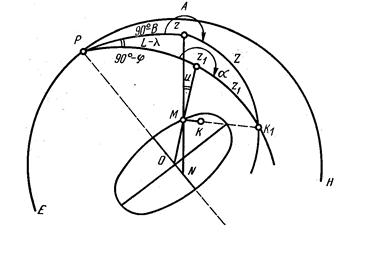
Рис. 5.2

На рис. 5.2 изображена вспомогательная сфера ЕРН. Радиус такой сферы произволен, но во много раз больше радиуса Земли (на рисунке масштаб не соблюден).

Р — полюс мира. Полюс мира можно представить как пересечение вспомогательной сферы продолжением оси вращения Земли. Продолжим нормаль и отвесную линию точки Земли М до их пересечения с вспомогательной сферой в точках Z и Z₁. Тогда, если МN — нормаль к эллипсоиду в точке М, то Z — геодезический зенит точки М; если МО — отвесная линия в точке М, то Z₁ —астрономический зенит точки М (точки Z и Z₁ расположены, конечно, не в плоскости чертежа).

Угол ZMZ₁ = и — уклонение отвесной линии в точке М; PZ — геодезический меридиан точки М; PZ₁ — астрономический меридиан точки М; К ₁ — точка пересечения визирной линии со вспомогательной сферой при наведении трубы теодолита на земной предмет К.

Угол при полюсе ZPZ₁ = L — λ — разность геодезической и астрономической долготы.

Связь между астрономическими и геодезическими координатами устанавливается через уклонения отвесных линий. Эта связь может быть представлена формулами

B = φ + Δφ, L = λ + Δλ,

где Δφ и Δλ — функции уклонений отвесных линий.

Геодезический азимут А вычисляют через астрономический при помощи уравнения Лапласа

А = α + (L — λ) sin φ.

В геодезических работах различиями между астрономическими и геодезическими координатами, как правило, не пренебрегают. В мелкомасштабных, например, картографических работах различиями между астрономическими и геодезическими координатами можно пренебречь, употребляя широты и долготы как координаты общей системы географических координат.

Редуцируя результаты геодезических измерений на поверхность референц-эллипсоида, приводим их к нулевой высоте, т. е. Н = 0. Этим существенно упрощаются дальнейшие вычисления. Вместо вычисления для всех точек координат В, L и Н, определяющих положение любой точки в пространстве, вычисляют только координаты В и L.

Дата добавления: 2014-01-15