Понятие сигнала и его модели

Математические модели сигналов

ЛЕКЦИЯ 2

Система шин

Интерфейс

а) Технические средства сопряжения функциональных блоков в систему

б) Программное обеспечение, определяющее порядок обмена информацией и порядок выполнения команд

1. ША – шина адреса
2. ШУ – шина управления
3. ШД – шина данных

В широком смысле слова под сигналом понимают материальный носитель информации: естественный или специально созданный.

В дальнейшем под сигналом будем понимать специально созданный сигнал для передачи сообщения в информационной системе.

Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем (переносчиком информации (сообщения)).

Носитель становится сигналом в процессе модуляции.

Параметры носителя, изменяемые во времени в соответствии с передаваемым сообщением, называют информационным.

В качестве носителя информации используются колебания различной природы, чаще всего гармонические, включая частный случай – постоянное состояние (w=0). В ИИС наибольшее распространение получили носители в виде электрического напряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности, будем соотносить их с электрическими сигналами.

Колебания принято подразделять на детерминированные и случайные.

Детерминированными называют колебания, которые точно определены в любые моменты времени.

Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.

При теоретическом изучении сигналов, исследовании их общих свойств мы отвлекаемся от их конкретной природы, содержания и назначения, заменяя моделями.

Модель – это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.

Модель позволяет установить количественные соотношения между основными параметрами, характеризующими исследуемый объект или процесс (в нашем случае сигнал).

Методы математического моделирования многообразия.

Фундаментальные исследования базируются на методе аналитического моделирования, заключающимися в создании совокупности математических соотношений, позволяющих выявить зависимости между параметрами модели в общем виде. При этом широко используются модели, параметры которых противоречат физическим свойствам реальных объектов. Например, модель сигнала часто представляется суммой бесконечного числа функций, имеющих неограниченную продолжительность (синусоид). Поэтому важно обращать внимание на условие, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.

Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать изменение значения информативного параметра невозможно. Следовательно, сигнал принципиально представляет собой случайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.

Тем не менее, детерминированные колебания рассматривают и в этом случае говорят о детерминированном сигнале. Ему соответствует модель в виде функции, полностью определенной во времени.

Изучение моделей детерминированных сигналов необходимо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются необходимыми для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный процесс, т.е. детерминированное колебание, представляет собой выраженную форму случайного процесса со значениями параметров, известными в любой момент времени с вероятностью, равной единице. Детерминированные сигналы имеют и самостоятельное значение. Они специально создаются для целей измерения, наладки и регулирования объектов информационной техники, выполняя роль эталонов.

Формы представления детерминированных сигналов.

В зависимости от структуры параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.

В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:

1) Непрерывная функция непрерывного аргумента (например, времени) (рис. 3, а);

2) Непрерывная функция дискретного аргумента, например, функция, значения которой отсчитывают только в определенные моменты времени (рис.3, б);

3) Дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис. 3, в);

4) Дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис. 3, г).

Для упрощения построения моделей сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.

Наиболее широкий класс исследуемых систем – это инвариантные во времени линейные системы.

При анализе прохождения сложного сигнала u (t) через такие системы его представляют в виде взвешенной суммы базисных функций j _k(t) (или соответствующего ей интеграла):

(1)

где [t₁, t₂] – интервал существования сигнала.

При выбранном наборе базисных функций сигнал u (t) полностью определяется совокупностью безразмерных коэффициентов С _к. Такие совокупности чисел называют дискретными спектрами сигналов.

На интервале [t₁, t ₂] выражение (1) справедливо как для сигналов неограниченных во времени так и для сигналов конечной длительности. Однако за пределами интервала [ t ₁,t₂] сигнал конечной длительности не равен нулю, т.к. он представляется суммой в том случае, если условно считается периодически продолжающимся. Поэтому, когда для ограниченного во времени сигнала необходимо получить представление, справедливое для любого момента времени, используется интеграл

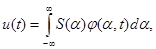(2)

где j (a, t) – базисная функция с непрерывно меняющимся параметром a.

В этом случае имеется непрерывный сплошной спектр сигнала, который представляется спектральной плотностью S ( a ). Разрешимость ее обработки размерности a. Аналогом безразмерного коэффициента С _к здесь является величина S (a)d a.

Совокупность методов представления сигналов в виде (1) и (2) называют обобщенной спектральной теорией сигналов. В рамках линейной теории спектра являются удобной формой представления сигналов.

Базисные функции j _k(t) должны быть просты, обеспечивать быструю сходимость ряда (1) для любых сигналов u (t) и позволять легко вытенять значения коэффициентов С _к. Базисные функции не обязательно должны быть действительными, их число может быть неограниченным (-¥ £ к £ ¥).

В случае практической аппроксимации реального сигнала совокупностью базисных сигналов решающее значение приобретает простота их технической реализации. Сигнал представляется суммой ограниченного числа (0 £ к £ n) действительных линейно независимых базисных функций (сигналов).

Ортогональное представление сигналов.

Вычисление спектральных составляющих сигнала значительно упрощаются при выборе в качестве базиса системы ортогональных функций.

Систему функций y₀(t), y₁(t),..., y_k(t),..., y_j(t),..., y_n(t) называют ортогональной на отрезке [t_a, t_b] если для всех k = o,n; j = o,n, за исключением случаев k = j, удовлетворяется условие

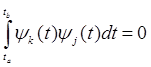(3)

эта система функций будет ортонормированной (ортонормальной), если для всех j = o,n справедливо соотношение

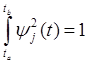(4)

Если (4) не выполняется и

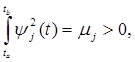
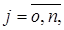
то систему можно нормировать, умножая функции y_j(t) на .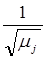

Определим коэффициенты С _k при представлении сигнала U (t) совокупностью ортонормированных функций в виде

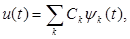
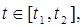(5)

предполагая, что интервал [t₁, t₂] лежит внутри отрезка ортонормальности [t_a, t_b].

Правую и левую части (5) умножаем на y_j(t) и интегрируем на интервале [t₁, t₂]:

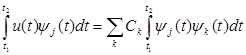(6)

В силу справедливости (3) все интегралы в правой части (6) при k ¹ j будут равны 0. При k = j в соответствии с (4) интеграл равен 1.

Следовательно

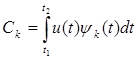(7)

В теоретических исследованиях обычно используются полные системы ортогональных функций, обеспечивающих сколь угодно малую разность непрерывной функции U(t) и представляющего ее ряда при неограниченном увеличении числа его членов. Разность оценивают по критерию

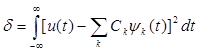(8)

При этом говорят о среднеквадратической сходимости ряда 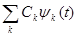к функции U(t).

Широко известной ортонормированной системой является совокупность тригонометрических функций кратных аргументов:

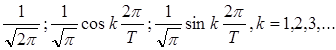
Она ортонормальна на отрезке [-p,p]. Т.к. соответствующее разложение исторически появилось первым и было названо рядом Фурье, то соотношения (5) часто именуют обобщенным рядом Фурье, а значения C_k – обобщенными коэффициентами Фурье.

Справка. В теории сигналов доказывается, что любой периодический сигнал U(t), имеющий на периоде конечное число точек разрыва первого ряда, может быть представлена в виде

(*)

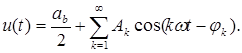Иными словами, периодический сигнал U(t) сложной формы может быть разложен на элементарные гармонические колебания с амплитудой А_к, частотой кw₁ и начальной фазой j_к. Здесь w₁ – круговая частота первой гармоники (Т₁=2p/w₁).

Если знать, что

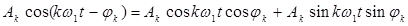
и ввести обозначение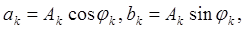

то выражение (*) примет вид

(**)

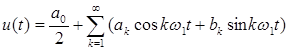Здесь А=U₀/2 представляет нулевую гармонику. Выражение (**) представляет разложение периодического сигнала U(t) в ряд Фурье. При этом коэффициенты ряда Фурье могут быть определены по формулам

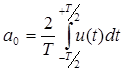
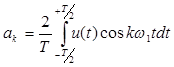
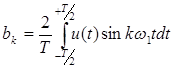
Легко заметить, что амплитуда А_к и начальная фаза j_к в разложении (*) равны

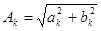и

Отметим важное свойство системы функций

cosw₁t, sinw₁t, cos2w₁t, sin2w₁t,...,coskw₁t, sinkw₁t, используемых в разложении (**). Это свойство состоит в том, что интеграл взятый от произведения любых двух функций на периоде Т=2p/w₁, равен нулю, т.е.

,

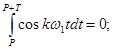
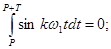
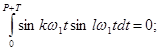
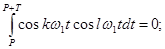
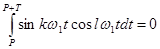где Р – действительное число; l – натуральное число (l ¹ к). Указанное свойство называется ортогональностью.

Дата добавления: 2014-01-15