Примеры. Обработка ошибок выражение 1 on error выражение 2

Обработка ошибок

выражение 1 on error выражение 2

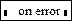
Если при вычислении значения выражения 2 возникла ошибка, то вычисляется значение выражения 1.

Пример. Составить функцию для вычисления значения выражения .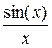

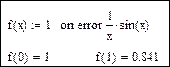
Пример. Дана последовательность чисел. Если в результате замены отрицательных элементов последовательности их квадратами, числа будут образовывать неубывающую последовательность, получить сумму членов исходной последовательности, в противном случае получить их произведение. Построить прямоугольную диаграмму исходной последовательности.

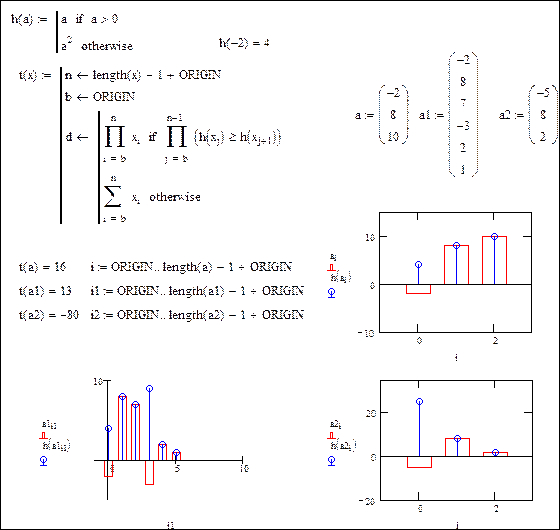
В примере используется вспомогательная функция h, которая возвращает исходное значение аргумента, если он положителен, и его квадрата в противном случае. Произведение 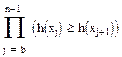принимает значение 1, если элементы вектора, получающегося после замены отрицательных элементов их квадратами, образуют убывающую последовательность.

На графиках исходный вектор представлен в виде прямоугольной диаграммы, а получающийся после замены отрицательных элементов квадратами – в виде решетчатой функции.

Пример.Составить функцию для взаимной перестановки строк, содержащих максимальный и минимальный элементы матрицы.Если перестановка выполнена, функция должна возвращать матрицу, получившуюся после перестановки. В противном случае результатом должно быть соответствующее сообщение.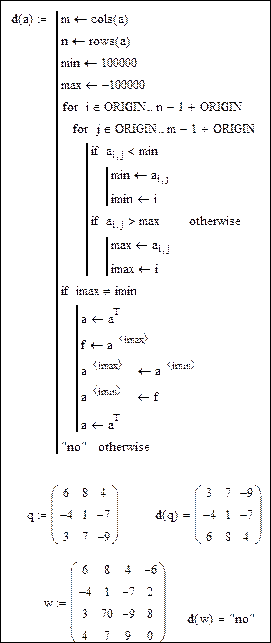

Пример. Дана действительная матрица. Требуется определить в каждой строке наименьший элемент, затем из минимальных элементов строк выбрать наибольший и определить индексы найденного элемента.   В программном блоке формируются вектора: min - минимальных значений каждой строки исходной матрицы; jmin – номеров столбцов, в которых расположены минимальные элементы строк матрицы. Решением является максимум минимальных элементов строк max и номер строки imax, в котором он расположен. Функция возвращает матрицу-строку, элементами которой является два вложенных вектора min и jmin, значение искомого элемента max и его индексы: imax – номер строки, jminimax.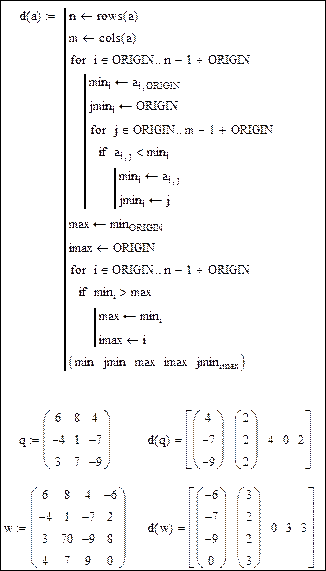

Пример. Определение значения интеграла методом Монте-Карло.

Идея метода. Пусть необходимо определить площадь 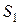некой фигуры на плоскости. Для этого ограничиваем заданную фигуру прямоугольной областью с координатами верхнего левого угла (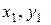) и правого нижнего (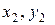), площадью 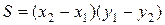. Задаем 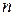точек на плоскости со случайными координатами, принадлежащих выбранному прямоугольнику и из них определяем количество точек 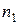, принадлежащих той части плоскости, площадь которой следует определить. Искомая площадь 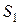пропорциональна количеству точек 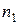и рассчитывается по формуле .

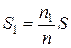Рассчитать площадь фигуры, ограниченной параболой и прямой:

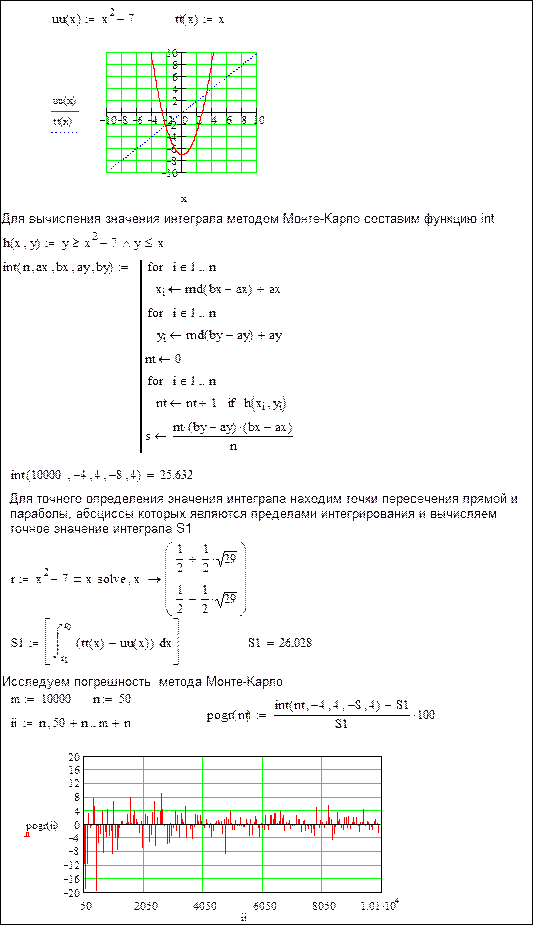
Пример. Сформировать матрицу размером 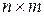и заполнить ее последовательными целыми числами от 1 до 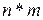, расположенными по спирали, начиная с верхнего левого угла, продвигаясь по часовой стрелке.

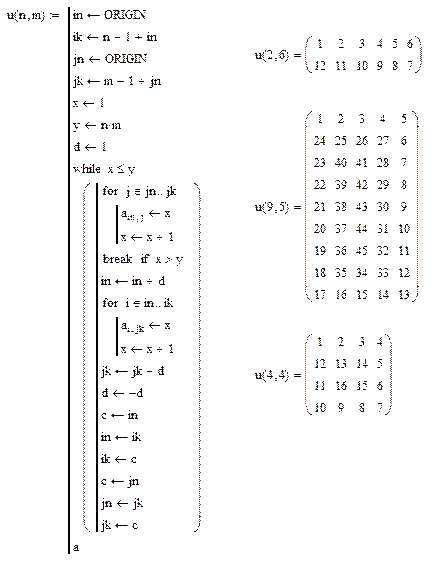
Пример. Найти максимальное из чисел, встречающихся в заданном векторе более одного раза.

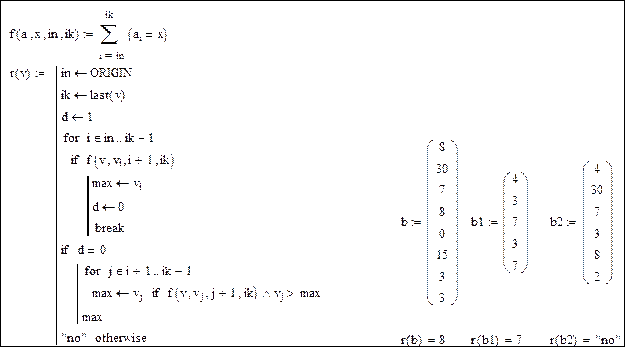
Приложение А

Дата добавления: 2014-01-15