Пример расчета статически неопределимой рамы на температурное воздействие методом перемещений

В раме, показанной на рис. 20.5,а, со стороны волокон, отмеченных пунктирной линией на горизонтальном и наклонном элементах, произошло изменение температуры: 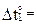–3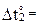0ºС, 40ºС, 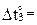20ºС. Коэффициент линейного температурного расширения материала, из которого изготовлены стержни рамы, известен и равен α. Поперечные сечения всех элементов рамы прямоугольные, их высота на горизонтальных участках рамы h_г равна 0,4 м, на наклонных – h_н = 0,25 м. Абсолютные значения изгибных жесткостей поперечных сечений элементов рамы известны: на горизонтальных участках – 12EJ, на наклонных – 5EJ, причем численное значение EJ задано. Требуется построить эпюры внутренних усилий от указанного температурного воздействия.

Воспользуемся некоторыми результатами расчета этой рамы на силовое воздействие (см. п. 19.7 девятнадцатой лекции).

1. Вычисление погонных жесткостей стержней рамы:

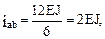
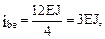
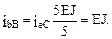
2. Определение степени кинематической неопределимости рамы и выбор основной системы метода перемещений (рис. 20.5,б).

3. Построение деформационных схем и соответствующих им эпюр изгибающих моментов M₁ и M₂ в единичных состояниях основной системы метода перемещений (рис. 19.18 и 19.19).

4. Вычисление коэффициентов при неизвестных системы канонических уравнений метода перемещений

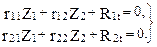(20.4)

В п. 19.7 девятнадцатой лекции коэффициенты при неизвестных r₁₁, r₁₂, r₂₁, r₂₂ системы уравнений (20.4) определены с использованием относительных изгибных жесткостей стержней рамы, т.е. при EJ=1 (см. рис. 19.21 и 19.22,а,б). С учетом заданного абсолютного значения EJ имеем:

r₁₁ = 19EJ, r₁₂ = r₂₁ = – 1,125EJ, r₂₂ = 2,2969EJ.

5. Определение перепадов приращений температуры по высоте поперечных сечений 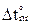и приращений температуры на уровне их центров тяжести 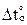(рис. 20.6) для элементов, где имеет место температурное воздействие.

Участок ab: 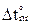= 40 – (–30) = 70 ºС,

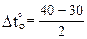= 5 ºС.

Участок bВ: 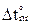= 20 – 0 = 20 ºС,

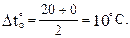
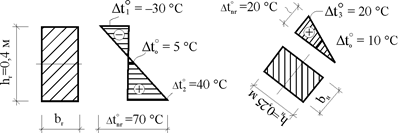
Рис. 20.6

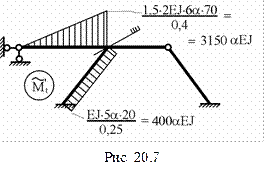6. Построение эпюры изгибающих моментов в основной системе метода перемещений от неравномерных приращений температуры 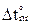(рис. 20.7). Для построения эпюры использованы стандартные задачи, приведенные в п. 20.1 настоящей лекции (см. рис. 20.2,д и 20.3,а).

7. Построение эпюры изгибающих моментов в основной системе метода перемещений от равномерных приращений температуры 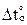(рис. 20.8,в). Для получения деформационной схемы от этого воздействия (рис. 20.8,а) предварительно построим план перемещений узлов рамы (рис. 20.8,б) с учетом абсолютных продольных перемещений стержней ab и bВ, вызванных нагреванием волокон на уровне центров тяжести их поперечных сечений

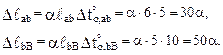
По плану перемещений (диаграмме Виллио) определим перекосы стержней от равномерного изменения температуры

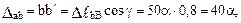
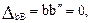
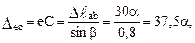
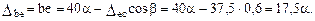
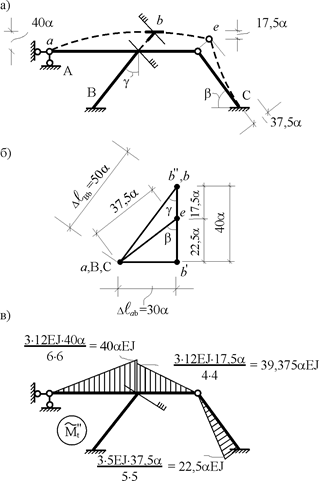
Рис. 20.8

Для получения ординат эпюры изгибающих моментов (рис. 20.8,в) использованы стандартные задачи, полученные от линейных перемещений узлов (см. рис. 19.9 и 19.10).

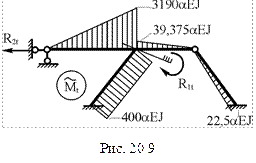8. Построение суммарной эпюры изгибающих моментов 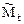=+от заданного изменения температуры в основной системе метода перемещений (рис. 20.9).

9. Определение свободных членов R_1t и R_2t системы канонических уравнений (20.4). Читателям предлагается, используя рис. 20.10,а,б, самостоятельно произвести вычисление этих коэффициентов. Из равновесия узлов, содержащих наложенные связи, получим:

R_1t = 2750,625αEJ, R_2t = 407,8912EJ.

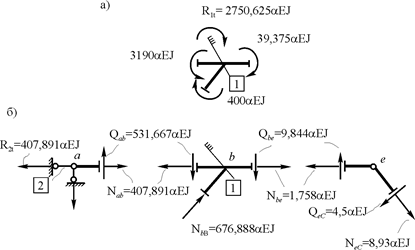
Рис. 20.10

10. Решение системы канонических уравнений (20.4)

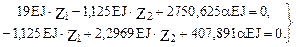
Z₁ = – 159,92α, Z₂ = – 255,91α.

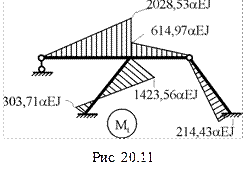11. Построение эпюр внутренних усилий M_t, Q_t, N_t в раме от заданного температурного воздействия. На рис. 20.11 показана только эпюра изгибающих моментов M_t, ординаты которой, как и следовало ожидать, зависят от абсолютных значений изгибных жесткостей поперечных сечений элементов рамы.

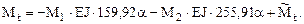
Так как коэффициенты при неизвестных r_11,, r₁₂, r₂₁, r₂₂ системы уравнений (20.4) определены с учетом абсолютных изгибных жесткостей поперечных сечений стержней, в последнем соотношении ординаты эпюр изгибающих моментов М₁ и М₂ в единичном состояниях основной системы метода перемещений (рис. 19.18 и 19.19) увеличены в EJ раз.

Эпюры поперечных Q_t и продольных сил N_t читатели, при необходимости, могут построить самостоятельно.

12. Статическая проверка правильности решения задачи. Используя необходимые условия равновесия для всей рамы, читатели могут убедиться в том, что они строго выполняются.

Дата добавления: 2014-01-15