Условные (импликативные) суждения. Полным или закрытым называют дизъюнктивное суждение, в котором перечислены все признаки или все виды определенного рода

Полным или закрытым называют дизъюнктивное суждение, в котором перечислены все признаки или все виды определенного рода.

Разделительные (дизъюнктивные) суждения.

Разделительным, или дизъюнктивным, называют суждение, со­стоящее из нескольких простых, связанных логической связкой «или».

Разделительное суждение может быть как двух-, так и многосо­ставным: р Ú q Ú r Ú… n

В языке разделительное суждение может быть выражено одной из трех логико-грамматических структур.

1) Разделительная связка представлена в сложном субъекте по схеме: S₁ или S₂ есть Р.

2) Разделительная связка представлена в сложном предикате по схеме: S есть P₁ или P₂.

3) Разделительная связка представлена сочетанием первых двух способов по схеме: S₁ илиS₂ есть P₁ или P₂.

Нестрогая и строгая дизъюнкция. Поскольку связка «или» упот­ребляется в естественном языке в двух значениях — соединительно-разделительном и исключающе-разделительном, то следует разли­чать два типа разделительных суждений: 1) нестрогую (слабую) ди­зъюнкцию и 2) строгую (сильную) дизъюнкцию.

1) Нестрогая дизъюнкция — суждение, в котором связка «или» употребляется в соединительно-разделительном значении (сим­вол v).

2) Строгая дизъюнкция — суж­дение, в котором связка «или» упот­ребляется в разделительном значе­нии (символ).

Члены строгой дизъюнкции, называемые альтернативами, не могут быть одновременно истинными.

Разделительная связка в языке обычно выражается с помощью союзов «или», «либо». С целью усиления дизъюнкции до альтерна­тивного значения нередко употребляют удвоенные союзы: вместо выражения «р или q» употребляют «или р, или q», а вместе «р либо q» — «либо р, либо q».Поскольку в грамматике отсутствуют одно­значные союзы для нестрогого и строгого разделения, то вопрос о типе дизъюнкции в юридических и других текстах должен решаться содержательным анализом соответствующих суждений.

Полная и неполная дизъюнкция. Среди дизъюнктивных сужде­ний следует различать полную и неполную дизъюнкцию.

Символически это суждение можно записать следующим образом:

<р v q v r>.

Например: «Леса бывают лиственные, хвойные или смешанные». Полнота этого разделения (в символической записи обозначается знаком <...>) определяется тем, что не существует, помимо указанных, других видов лесов.

Неполным или открытым называют дизъюнктивное суждение, в котором перечислены не все признаки или не все виды определен­ного рода. В символической записи неполнота дизъюнкции может быть выражена многоточием:

р v q v r v...

В естественном языке не­полнота дизъюнкции выражается словами: «и т.д.», «и др.», «и тому подобное», «иные» и другими.

Условным, или импликативным, называют суждение, состоя­щее из двух простых, связанных логической связкой «если.., то...». Например: «Если предохранитель плавится, то электролампа гас­нет». Первое суждение — «Предохранитель плавится» называют антецедентом (предшествующим), второе — «Электролампа гас­нет» — консеквентом (последующим). Если антецедент обозначить р,консеквент — q, а связку «если..., то...» знаком «®», то имплика-тивное суждение символически можно выразить как р®q.

В естественном языке для выражения условных суждений ис­пользуется не только союз«если..., то...», но и другие союзы: «там..., где», «тогда..., когда...», «постольку..., поскольку...» и т.п. В форме условных суждений в языке могут быть представлены такие виды объективных связей, как причинные, функциональные, про­странственные, временные, правовые, а также семантические, логи­ческие и другие зависимости. Примером причинного суждения может служить следующее высказывание: «Если воду нагреть при нормальном атмосферном давлении до 100°С, то она закипит». При­мер семантической зависимости: «Если число делится на 2 без остат­ка, то оно четное».

В форме условных суждений нередко выражают логические зави­симости между высказываниями. Например: «Если верно, что некоторые птицы улетают зимой в теплые края, то неверно, что ни одна птица не улетает в теплые края».

В условном суждении антецедент выполняет функцию фактичес­кого или логического основания, обусловливающего принятие в консеквенте соответствующего следствия. Зависимость между антеце­дентом-основанием и консеквентом-следствием характеризуется свойствомдостаточности. Это означает, что истинность основания обусловливает истинность следствия, т.е. при истинности осно­вания следствие всегда будет истинным. При этом основание не характеризуется свойством необхо­димости для следствия, ибо при его ложности следствие может быть как истинным, так и ложным.

4. Эквивалентные суждения (двойная импликация). Эквивалентным, называют суждение, включающее в качестве составных два суждения, связанных двойной (прямой и обратной) условной зависимостью, выражаемой логической связкой «если и только если..., то...». Например: «Если и только если человек на­гражден орденами и медалями (р), то он имеет право на ношение соответствующих орденских планок (q)».

Логическая характеристика этого суждения состоит в том, что истинность утверждения о награждении (р) рассматривается как необходимое и достаточное условие истинности утверждения о на­личии права на ношение орденских планок (q). Точно так же истин­ность утверждения о наличии права на ношение орденских планок (q) является необходимым и достаточным условием истинности ут­верждения о том, что данное лицо награждено соответствующими орденом или медалью (р).

В естественном языке для выражения эквивалентных суждений используют союзы: «лишь при условии что..., то...», «в том и только в том случае когда..., тогда...», «только тогда когда..., то...» и другие.

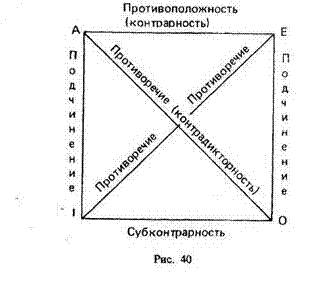
22)Логический квадрат” представляет собой наглядную схему взаимного отношения суждений четырех типов А, Е, I, О. Строится логический квадрат так: левый верхний угол обозначается буквой А (общеутвердительное суждение) или SaP; правый верхний угол обозначается буквой Е (общеотрицательное суждение) или SeP; нижний левый угол обозначается буквой I (частноутвердительное суждение) или SiP; нижний правый угол обозначается буквой О (частноотрицательное суждение) или SoP.

Каждая линия, соединяющая выделенные типы суждений, представляет определенное отношение между двумя типами суждений. Византийский логик XI в. Михаил Пселл, предложивший “логический квадрат”, обратил внимание на то, что, зная истинность или ложность одного суждения в схеме “логического квадрата”, можно сделать вывод об истинности или ложности другого суждения.

Логический квадрат

В самом деле, мы уже знаем закон противоречия, который был использован нами в логике высказываний: противоречащие друг другу высказывания не могут быть вместе истинными. Если я высказываю общеутвердительное суждение SaP “Все студенты хорошо подготовились к зачету”, то, утверждая истинность общеутвердительного суждения, тем самым отрицаю истинность частноотрицательного суждения SoP “Некоторые студенты не подготовились к зачету”. И, наоборот, утверждая истинность частноотрицательного суждения, я отрицаю истинность общеутвердительного суждения.

То же будем иметь, если я буду утверждать истинность общеотрицательного суждения SeP. Тем самым я не признаю истинность частноутвердительного суждения SiP “Некоторые студенты подготовились к зачету по логике”.

Итак, противоречащими друг другу суждениями будут пары суждений А и О и Е и I. Они, в соответствии с законом противоречия, не могут быть одновременно истинными. И, тем более, не могут быть одновременно истинными контрарные (противоположные) суждения А и Е (А: “Все студенты подготовились к зачету” и Е: “Ни один студент не подготовился к зачету”).

Все сказанное нами дает возможность сделать следующий вывод об истинности суждений:

если истинно А, то ложно О и ложно Е;

если истинно Е, то ложно I и ложно А;

если истинно I, то ложно Е;

если истинно О, то ложно А.

Теперь попробуем рассуждать от ложности. Здесь мы должны воспользоваться законом исключенного третьего. Этот закон запрещает одновременную ложность противоречащих друг другу суждений.

Отсюда мы должны сделать следующий вывод:

если ложно А, то истинно О;

если ложно О, то истинно А;

если ложно Е, то истинно I;

если ложно I, то истинно Е.

К этим выводам можно добавить вывод, полученный косвенно: например, пусть А истинно. Что можно сказать об истинности I? Нетрудно доказать с помощью наших законов мышления, что истинность общего суждения будет обозначать истинность частного суждения.

Если истинно А, то на основании закона противоречия будет ложным Е. Но если ложно Е, то на основании закона исключенного третьего будет истинно I. Значит, если истинно А, то истинно I. Аналогично можно доказать, что истинность Е обуславливает истинность О.

В самом деле, если Е истинно, то, на основании закона противоречия, А ложно. Если А ложно, то на основании закона исключенного третьего, О истинно. Значит, если истинно Е, то истинно О.

Отсюда следует общий вывод: если общее суждение А или Е истинно, то будет истинным и подчиненное им частное суждение, соответственно, I и О. Здесь следует еще раз напомнить читателю, что термин “некоторые” в логике суждений используется не в смысле “некоторые, но не все”, а в смысле “некоторые, может быть, и все”.

Далее, рассмотрим те высказывания, которые могут быть получены из ложности частных суждений. Допустим, I — ложно. Тогда, на основании закона исключенного третьего, Е истинно. На основании закона противоречия в этом случае А ложно. Применяя закон исключенного третьего к противоречащему суждению, получим, что О истинно. Значит, мы получили вывод о том, что ложность частного суждения 1 обуславливает ложность общего А и истинность субконтрарного суждения О.

Соответственно, если ложно О, значит, истинно А и ложно Е, и истинно I.

Значит, ложность частного суждения О обуславливает ложность общего суждения Е и истинность субконтрарного суждения 1.

Из этого следует, соответственно, два вывода:

1) ложность частного суждения обуславливает ложность общего суждения;

2) ложность частного суждения обуславливает истинность субконтрарного частного суждения.

Мы рассмотрели все выводы, которые можно получить по схеме “логического квадрата”. Однако, важно так же иметь в виду те выводы, которые нельзя получить.

Нельзя получить вывод от ложности общего к ложности частного суждения.

Нельзя получить вывод от истинности частного суждения к истинности общего суждения.

И, наконец, нельзя перейти от ложности общего к истинности контрарного (противоположного) суждения, т. е. нельзя распространять закон исключенного третьего на контрарную противоположность.

Если ложно А, то отсюда никак не следует истинность Е, так же, как из ложности Е не следует истинность А.

Известен с древних времен так называемый парадокс Эпименида, который был критянином. И он сказал: “Все критяне лгуны”. Поскольку он критянин, то, оказывается, что и он лгун. Значит, критянин говорит правду. Следовательно, он — лжец, поскольку его утверждение, что “Все критяне лгуны” — ложно. А раз оно ложно, то значит, критяне говорят правду. И он, как критянин, говорит правду. Значит, что “все критяне — лгуны” — истинно.

Одно и то же суждение и истинно, и ложно, и это противоречит нашим законам мышления.

Зная изложенные выше правила, относящиеся к законам мышления, нам легко разобраться в этом парадоксе. Пусть утверждение “Все критяне лгуны” — ложно. Это общеутвердительное суждение А. Однако, в соответствии с законом исключенного третьего, из ложности А никоим образом не следует, что критяне говорят правду, т. е. истинность Е (Ни один критянин не лгун). Может быть, какие-то критяне не лгуны, и тогда парадокс исчезает.

Отметим, что столь простое исчезновение парадокса лжеца возможно лишь в том случае, когда он дан в приведенной выше форме (парадокс Эпименида). Значительно более сложной является ситуация парадокса Эвбулида: “То, что я сейчас вам говорю, — ложь”! Однако, есть попытки решения парадокса и в этом случае.

Отношения между простыми суждениями обычно иллюстрируют с помощью схемы, получившей название логического квадрата. Логический квадрат (квадрат противоположностей) - это диаграмма, служащая для мнемонического запоминания логических отношений между видами суждений по объединенной классификации.
Вершины квадрата обозначают вид суждения по объединенной классификации А, Е, 0, I. Стороны и диагонали символизируют логические отношения между простыми суждениями (кроме эквивалентных). Верхняя сторона есть отношение А и Е - противоположность (контрарность); нижняя сторона - отношение между I и O - частичная совместимость (субконтрарность); две вертикальные стороны - отношения между А и I (левая), Е и О (правая) - подчинение; диагонали - отношения между А и О, Е и I- противоречие (контрадикторность).
б) Отношения между суждениями с отношениями различают следующие:
1) Реляционные суждения (или суждения об отношениях между предметами мысли), имеют нечто общее с атрибутивными суждениями: трехчленность строения, наличие количества и качества. Поэтому они могут находиться тоже в отношениях подчинения, частичной совместимости, противоположности, противоречия или же логической независимости.
В то же время реляционные суждения отличаются от атрибутивных тем, что раскрывают не свойства предметов, а отношения между предметами и, следовательно, имеют не одночленный (одноместный) предикат, а многочленный (n-местный от двух и более). Поэтому в зависимости от характера отношения между предметами и внутри суждения устанавливаются свои, особые отношения. Они могут быть: симметричными (отношения между предметами, для которых не имеет значения, какой из этих членов предшествующий, а какой последующий; например: “Иван - брат Петра”, следовательно, “Петр - брат Ивана”) и несимметричными (отношения между предметами, при которых важен порядок их расположения; например: “Иван - отец Степана”, но это не значит, что “Степан - отец Ивана”, если истинно одно из этих суждений, то ложно другое.).
2) Транзитивные (или переходные отношения). Если, например, 1 предмет эквивалентен 2-му, а 2-й эквивалентен 3му, то и 1-й эквивалентен 3-му. Это могут быть также отношения величины (больше - меньше), пространственные (дальше - ближе) и др. Например: “Иван - брат Петра”, “Петр - брат Елены”, значит, “Иван - брат Елены”. Такие суждения либо одновременно истинны, либо одновременно ложны.
3) Нетранзитивные (непереходные) отношения обладают обратной зависимостью по сравнению с предыдущей. Так, если “Иван - отец Степана”, а “Степан - отец Николая”, то это не значит, что “Иван - отец Николая”. Он ему дед, следовательно, такие суждения не могут быть одновременно истинными.
4) Рефлексивные отношения характеризуются тем, что каждый из член отношения, находятся в таком же отношении к самому себе. Если два события произошли одновременно, то они одновременны между собой. Оба суждения могут быть либо истинными, либо ложными.
5) Нерефлексивные таковы, что если 2 меньше 3, то это не значит, что 2 меньше 2 и 3 меньше 3. Из истинности одного следует ложность другого.
2. Отношения между сложными суждениями.
Сложные суждения - аналогично простым - находятся в определенных отношениях между собой. Общим здесь является то, что они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми, причем и для них характерны отношения именно по их истинности или ложности. Однако отношения между сложными суждениями в известной мере специфичны. Обусловлено это их особой, более сложной и качественно иной структурой, отличной от структуры простых суждений.
а) Сравнимые среди сложных - это суждения, которые имеют одинаковые составляющие и различаются типами логических связок, включая отрицание: например, "Норвегия или Швеция являются членами НАТО" и "Неверно, что Норвегия и Швеция являются членами НАТО". Сравнивать эти суждения можно потому, что у них общие составляющие, хотя по логической форме они отличаются друг от друга: первое из них дизъюнктивное суждение (это связь двух и более простых суждений с помощью логических связок «или», «либо»), второе - отрицание конъюнкции (связь двух и более простых суждений с помощью логической связки «и»). Наличие общих составляющих позволяет сопоставлять их по смыслу и установить зависимости по истинности.
б) Несравнимыми среди сложных суждений являются суждения, которые частично или полностью различаются составляющими их суждениями. Например, нельзя сравнивать следующие два суждения: "Слух обо мне пройдет по всей Руси великой, и назовет меня всяк сущий в ней язык, и гордый внук славян, и финн, и ныне дикой тунгус, и друг степей калмык" и "Чем дальше в лес, тем больше дров". Различия в составляющих не позволяют установить смысловую и истинную зависимость между суждениями.
Между сложными суждениями складываются такие же виды отношений, как и между простыми. Характер этих отношений определяется с помощью таблиц истинности.

Суждения, как и понятия, делятся на сравнимые (имеют об­щий субъект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.

В математической логике два высказывания р и q называются несовместимыми, если из истинности одного из них необходимо следует ложность другого (т. е. p и q никогда не могут оказаться одновременно истинными). «Это понятие легко распространить на любое число высказываний: высказывания р₁ , р₂ ,..., р_n, называ­ются несовместимыми, если не может оказаться, что все они являются одновременно истинными»¹².

Совместимые выражают одну и ту же мысль полностью или лишь в некоторой части. Отношения совместимости: эквивален­тность, логическое подчинение, частичное совпадение (субконтрарность). Совместимые эквивалентные суждения выражают од­ну и ту же мысль в различной форме («Юрий Гагарин — первый космонавт» и «Юрий Гагарин первым полетел в космос»). Субъ­ект здесь один и тот же, а предикаты различные по форме, но одинаковые по смыслу. В двух эквивалентных суждениях: «Миха­ил Шолохов — лауреат Нобелевской премии» и «Автор романа «Тихий Дон» — лауреат Нобелевской премии» — одинаковыми являются предикаты, а различными по форме выражения, но тождественными понятиями — субъекты. Если два высказыва­ния эквивалентны, то невозможно, чтобы одно из них было истинным, а другое ложным.

В сочинении, при заучивании материала, в устном изложении текста, при переводе с одного языка на другой — всюду учащиеся должны уметь кратко и корректно излагать свои мысли. А. П. Чехов дал такое сравнение: «Краткость — сестра таланта».

Совместимые суждения, находящиеся в отношении логичес­кого подчинения, имеют общий предикат; понятия, выражающие субъекты двух таких суждений, также находятся в отношении логического подчинения. Отношения между суждениями по ис­тинности принято схематически изображать в виде «Логического квадрата»

23) Между суждениями существуют логические отношения. Суждения как и понятия, могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть существенные различия, вызванные их различной логической структурой. Если сравнимые понятия соотносятся друг с другом по их объему, то между сравнимыми суждениями имеются многообразные отношения прежде всего по их истинностным значениям. Анализ этих отношений предполагает выяснение таких вопросов: могут ли рассматриваемые суждения быть вместе истинными, вместе ложными, обусловливает ли истинность одного истинность другого и ложность одного ложность другого. Такой анализ имеет важное теоретическое и практическое значение, но его осуществление имеет свою специфику относительно простых и сложных суждений, поскольку они различаются своей логической структурой.

Дата добавления: 2014-01-15