Дотична площина та нормаль

План.

Библиографический список

1. Львов, Д.С. Институциональная экономика: Учебник. – М.: ИНФРА-М, 2001. – 318 с.

1. Частинні та повний прирости функції двох змінних (*).

2. Диференційовність функції двох змінних (*).

3. Геометричний зміст частинних похідних (*).

4. Достатня умова диференційовності функції двох змінних у точці (*).

5. Диференціювання функцій (**).

6. Дотична площина та нормаль (**).

7. Частинні похідні і повні диференціали вищих порядків (**).

20.1 Частинні та повний прирости функції двох змінних.

Нехай функція визначена в деякому околі точки 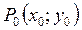. Надамо незалежним змінним x та y приросту відповідно та 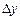так, щоб точка не виходила за межі вказаного околу. Тоді й точки 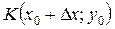, 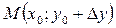також належатимуть розглядуваному околу.

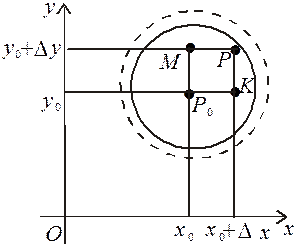
Різницю 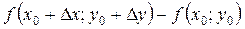називають повним приростом функції при переході від точки 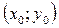до точки і позначають 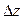. Різницю 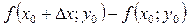називають частинним приростом за х, а різницю — частинним приростом за y функції ; їх позначають відповідно і .

Таким чином,

,

,

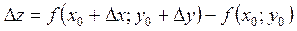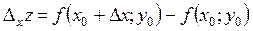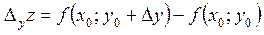
Аналогічно визначаються прирости функції більш ніж двох змінних.

20.2 Диференційовність функції двох змінних.

Означення. Функція 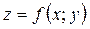називається диференційовною у точці 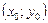, якщо її повний приріст 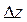можна подати у вигляді:

,

де А, В — числа, a, b — нескінченно малі при .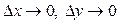

Головна лінійна частина приросту функції, тобто називається повним диференціалом функції (точніше першим дифе­ренціалом) двох змінних у точці 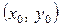і позначається

.

Теорема. Якщо функція 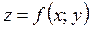диференційовна в точці 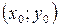, тоді існують границі 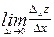та і вони дорівнюють відповідно А і В.

Означення. Нехай функція 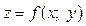визначена в точ-
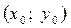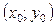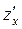ці і в її деякому околі. Якщо існує границя , то вона називається частинною похідною за х (за у) функції у точці і позначається , або , або .

Таким чином, , .

Із означення частинних похідних матимемо, що вони шукаються за тими правилами, що й похідні функції однієї змінної. Треба лише пам’ятати, що при знаходженні 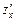змінна у вважається сталою, а при знаходженні 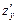змінна х вважається сталою.

Тепер можна теорему можна сформулювати таким чином:

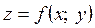Теорема. (необхідна умова диференційовності функції у точці). Якщо функція диференційовна в точці 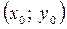, то в цій точці існують частинні похідн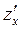і і .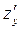

Диференціали незалежних змінних збігаються з їхніми приростами: 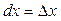, . Тоді, як випливає із означення повного диференціала і розглянутої теореми повний диференціал функції 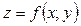можна обчислити за формулою:

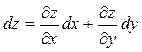
Аналогічно повний диференціал функції трьох аргументів 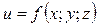обчислюється за формулою:

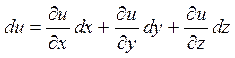
Приклад. Знайти , якщо .

Тоді:

, де ;

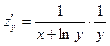
Отже,

.

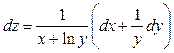20.3 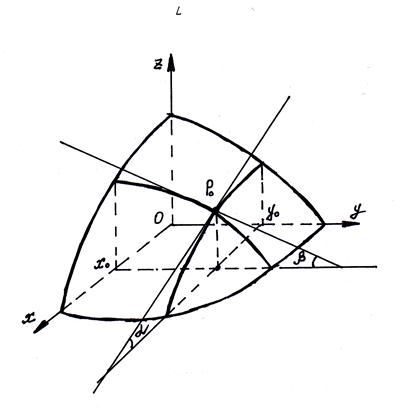Геометричний зміст частинних похідних.

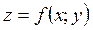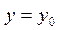Якщо функцію , що має частинні похідні в точці , розглядати за умови , то геометрично це означає, що поверхня перетинається площиною , паралельно координатній площині 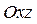; у перерізі дістаємо лінію. Тоді є кутовим коефіцієнтом дотичної до зазначеного перерізу в точці , тобто тангенсом кута нахилу цієї дотичної до додатного напряму осі Ох. Аналогічно, є кутовим коефіцієнтом дотичної, що проходить через точку , до кривої, яка утворюється в результаті перетину поверхні 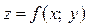з площиною .

20.4 Достатня умова диференційовності функції двох змінних у точці.

Для функції однієї змінної твердження щодо її диференційовності та існування похідної є рівносильними. У випадку функції двох змінних ми маємо інше: існування частинних похідних — необхідна умова диференційовності функції в точці, але не є достатньою умовою диференційовності.

Теорема. Якщо функція 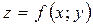у деякому околі точки має неперервні частинні похідні, тоді вона диференційовна в точці .

Можна навести твердження про зв’язок між поняттями неперервності і диференційовності функції двох змінних у точці, аналогічні до тих, що виконуються для функції однієї змінної.

Теорема. Якщо функція диференційовна в точці , то вона неперервна в цій точці.

Обернене твердження неправильне.

20.5 Диференціювання функцій.

20.5.1 Похідна неявної функції.

Якщо існує неперервна функція однієї змінної 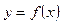, така що відповідні пари задовольняють умову , тоді ця умова називається неявною формою функції 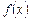, а сама функція 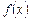називається неявною функцією, яка задовольняє умову .

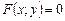Припустимо, що неперервна функція 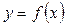задана в неявній формі і що 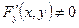. Похідну 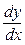обчислюємо за формулою:

,

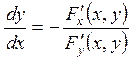Приклад. Знайти похідну від неявної функції –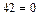в точці , .

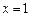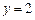Маємо 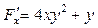, , звідки

.

Для , маємо .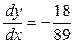

Аналогічно частинні похідні функції двох незалежних змінних 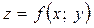, яку задано за допомогою рівняння 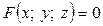, де — диференційовна функція змінних x, y, z, можуть бути обчислені за формулами:

, , за умови, що .

Приклад. Знайти 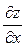, , 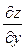якщо .

У даному разі 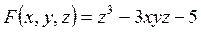. Знайдемо , , .

, , .

Тоді:

, .

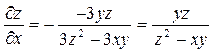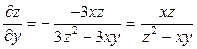20.5.1 Похідна складної функції.

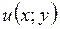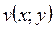Теорема. Нехай на множині D визначена складна функція , де , і нехай функції , мають у деякому околі точки неперервні частинні похідні, а функція — неперервні частинні похідні в деякому околі точки 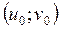, де , . Тоді складна функція диференційовна в точці , причому

Приклад. Знайти 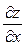і 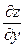для функції .

Маємо де .

Тоді , , , , , .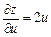

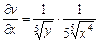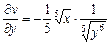Таким чином, , , або після підставляння виразів u і v дістанемо , .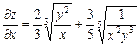

Якщо функція диференційовна в точці , то виконується рівність

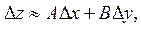
або

Узявши в цій наближеній рівності , , дістанемо:

На отриманій формулі ґрунтується алгоритм використання диференціала для наближених обчислень.

Крім того, якщо взяти , , дістанемо:

Це рівняння дотичної площини, що проходить через точку .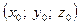

Якщо поверхню задано у просторі рівнянням , то рівняння дотичної площини до поверхні в точці має вигляд:

,

де , , .

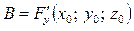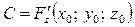Нормаль до поверхні в точці 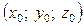— це пряма, що проходить через точку і перпендикулярна до дотичної площини.

Отже, її рівняння

.

20.7. Частинні похідні і повні диференціали вищих порядків.

Нехай функція має частинні похідні в усіх точках множини . Візьмемо будь-яку точку 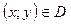; у цій точці існують частинні похідн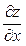і і 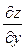, які залежать від x і y, тобто вони є функції двох змінних. Отже, можна ставити питання про знаходження їхніх частинних похідних. Якщо вони існують, то називаються похідними другого порядку і позначаються так:

або ,

або ,

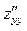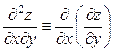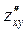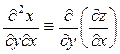або ,

або .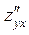

Аналогічно визначаються і позначаються частинні похідні третього і вищих порядків, наприклад:

, .

Означення. Диференціалом другого порядку від функції називається диференціал від її повного диференціала першого порядку, тобто .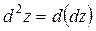

Аналогічно визначаються диференціали третього і вищих порядків

..........

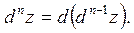
Приклад. Знайти , якщо .

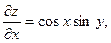
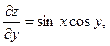
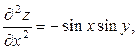
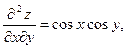
Приклад. Знайти і для функції .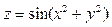

, ,

, .

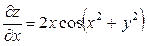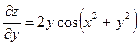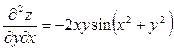У попередньому прикладі ми дістали, що . Виявляється, що ця рівність виконується в багатьох випадках, що випливає з такої теореми.

Теорема. Якщо функція 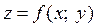визначена в області D і в цій області існують перші похідні 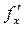та , а також другі мішані похідні , , 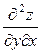які до того ж як функції від х і у неперервні в точці , то в цій точці:

.

Контрольні запитання.

1. Що називається частинними похідними та повним приростом функції двох змінних?

2. Сформулювати необхідну і достатню умови диференційованності функції двох змінних.

3. Поясніть геометричний зміст частинних похідних.

4. Записати рівняння дотичної площини та нормалі до певної поверхні в певній точці.

Дата добавления: 2014-01-15